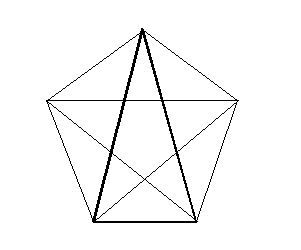
正五角形を作図するということはどういうことかというと, 図の --- といっても本当の正五角形を tool 無しで正確に描くのは難しいので, 本当の正五角形にはなってないと思うが --- 太く描いてある二等辺三角形を作図することと等しい。 --- やっぱり不正確だ (笑)。

何故かと言うと, 与えられた線分を底辺とし, この二等辺三角形を描けば, あとはその頂点を中心とし与えられた線分の長さを半径とする円を描き, 底辺の両端を中心とする同じ半径の円を描けば, それらの交点が残りの五角形の二つの頂点となるからである。
そこでこの二等辺三角形をもう少し良く調べてみよう。
この正五角形の外接円を描き, 中心と各頂点と結ぶと, この中心角は 360 度を 5 で割るのだから, 72 度である。 従って, 上記の二等辺三角形の頂角は, これの半分だから 36 度。 底角は (180 - 36) ÷ 2 = 72 [度]。 ということで, 一方の底角の二等分線を引いて図のような三角形を作るとそれはもとの三角形と相似になる。
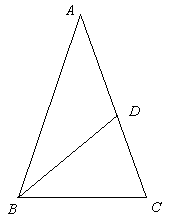
つまり △ABC ∽ △BDC. そしてすぐ分かるように ∠BAD = ∠DBA = 36度 だから, AD = BD = BC である。 そこで, BC の長さを 1 とした場合, AB = x がその何倍に当たるかを計算することにする。 今の話から CD = AC - AD = x - 1 である。 三角形の相似から, AB : BC = BC : CD だから
AB・CD = BC2.
即ち x(x -1) = 1. 展開して移項すると x2 - x - 1 = 0 を得る。 これから解の公式に入れて x = (1 ± √5)/2 であるが, 明らかに x > 1 なので x = (1 + √5)/2 である --- 所謂黄金比 golden ratio.
これから 72 度の余弦を計算すると
cos 72゜ = (1/2)/AB = 1/(2AB) = 1/(1 + √5) = ( √5 - 1)/((√5 - 1)(√5 + 1)) = ( √5 - 1)/(5 - 1) = ( √5 - 1)/4
である。 (ここで公式 (a + b)(a - b) = a2 - b2 を用いた) これは実は五次方程式 x5 - 1 = 0 を解いても得られる (こちら)。
さて, 問題は長さ 1 から長さ (1 + √5)/2 を作図することだが, 1/2 は垂直二等分線が作図できるから良い。 問題は √5/2だが, これを √(5/4) = √((1/4 + 1)) = √((1/2)2 + 12) とすれば, 要するに, 二辺の長さが 1, 1/2 であるような長方形の対角線を描けばいいわけだから, これは簡単である。
普通, BC の垂直二等分線を引き, 中点を M とする。 M から長さ 1 の点 E を採り, BE を結ぶ。 これで BE = √5/2. 更に, BE を延長して, EF = BM = 1/2 になるように採る。 これで BF = (1 + √5)/2. これを半径とし, B を中心とする円を描いて, BC の垂直二等分線との交点を求めると, それが上の図での A に当たるわけである。 これで正五角形が作図できたことになる。
与えられた円の中に正五角形を描くには次のようにする。 (細かい説明は省略する)
円の中心を O (半径を 1 としよう), 二つの直交する直径を AB, CD とする。 AO の中点 R と C を結ぶ (AR = CR = 1/2 より, CR = √5/2)。 R を中心とし, RC を半径とする円を描いて, OB との交点を W とする OW = CR - OR = ( √5 - 1)/2)。 今度は C を中心とし, CW を半径とする円を描き, 元の円との交点を M とすると, CM が求める正五角形の一辺になる。 つまり CM = CW = √(OW2 + 1) = √(10 - 2√5)/2. これの半分が sin 36゜ の逆数になっていることを確認すればいい。
[原始五乗根]
方程式 x5 - 1 = 0 を実際に解いてみよう。 先ず x - 1 で因数分解できて
x5 - 1 = (x - 1)(x4 + x3 + x2 + x + 1) = 0.
勿論興味があるのは x4 + x3 + x2 + x + 1 = 0 の方だ。 この左辺は円周等分多項式 cyclotomic polynomial と呼ばれる特殊な多項式である。 当然 x ≠ 0 であるから, x2 で割る (即ち x-2 を掛ける) と
x2 + x + 1 + x-1 + x-2 = 0.
x2 + x-2 + x + x-1 + 1 = 0.
ここで t = x+ x-1 と置く。 t2 = x2 + 2xx-1 + x-2 = x2 + x-2 + 2 より x2 + x-2 = t2 - 2. 従って
t2 - 2 + t + 1 = 0.
t2 + t - 1 = 0.
解の公式から解くと t = (-1 ± √5)/2. t = x+ x-1 だったから x+ x-1 = (-1 ± √5)/2. 両辺に x を掛けて移項すると
x2 - ((-1 ± √5)/2)x + 1 = 0
2x2 - (-1 ± √5)x + 2 = 0.
再び解の公式に入れて x = [(-1 + √5) ± √(-10 - 2√5)]/4, [(-1 - √5) ± √(-10 + 2√5)]/4. で, 2√5 < 10 だから, 虚数単位 i を用いると
x = [(-1 ± √5) ± i√(10 ± 2√5)]/4 (√5 の直前の複号だけ同順) となる。 複素平面を考えて cos(2π/5) = ( √5 - 1)/4, sin(2π/5) = √(10 + 2√5)/4 が分かる。