正接定理というのは △ABC に於て (a - b)/(a + b) = tan((A - B)/2)/tan((A + B)/2) が成り立つという一寸変わった定理である (岩波数学辞典 3/e には Napier の公式として出ている)。
普通この証明は三角函数の積を和に直す公式を用いて
rhs = 2sin((A - B)/2)cos((A + B)/2)/(2sin((A + B)/2)cos((A - B)/2))
= (sin A - sin B)/(sin A + sin B)
外接円の半径を R として, 正弦定理から
(sin A - sin B)/(sin A + sin B) = (R sin A - R sin B)/(R sin A + R sin B) = lhs.
というように行われる。
これを幾何学的に証明すると次のようになる。
a - b を考えるから BC ≧ CA としておく (そうでなければ, 入れ替えてから最後にもう一度入れ替え直せばよい)。
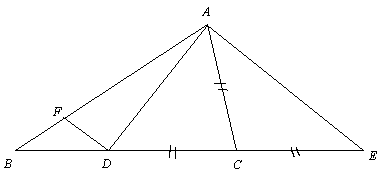
辺 BC 及びその延長上に点 D, E を CD = CE = CA となる様にとり, D から AE に平行な直線を引いて AB との交点を F とする。

△ADE は点 C を外心とする三角形だから ∠DAE = ∠R.
従って ∠ADF = 2∠R - (∠FDB + ∠ADE) = 2∠R - (∠AED + ∠DAC)
= 2∠R - (∠CAE + ∠DAC) = 2∠R - ∠DAE = ∠R.
△ABC の外角で ∠ACE = A + B. 従って
∠EDA = (A + B)/2.
∠DAF = A - ∠CAD = A - ∠EDA = (A - B)/2.
△ADF で tan((A - B)/2) = tan ∠DAF = DF/AD.
△ADE で tan((A + B)/2) = tan ∠EDA = AE/AD.
従って
tan((A - B)/2)/tan((A + B)/2)
= (DF/AD)/(AE/AD)
= DF/AE = BD/BE … △BAE ∽ △BFD
= (BC - CD)/(BC + CE) = (a - b)/(a + b).