Euclid 以来, 定木とコンパスとによる平面の作図を普通 「作図」 という。
ギリシャの三大作図不可能問題というのがあって, それは次のようなものである。
ここで扱うのは 1 だけであるが, 1 と 2 は同様の問題で, 共に P.-L. Wantzel (ワンツェル) が 1837 年に不可能だということを証明している (勿論, 直角や 45 度のような特殊な角は除く)。 又 3 の不可能性は C. L. F. Lindemann (リンデマン) によって 1882 年に不可能性が証明されている。
実は角の三等分及び立方体倍積は, 直角定木とコンパスがあれば解ける (L. Bieberbach)。 又円ではない二次曲線 (つまり楕円か双曲線) が描かれているときには定木とコンパスだけでこの二つの問題は解ける (H. J. S. Smith, H. Kortum) ということが知られている。
実は, 二箇所に印のついた物差し (これは普通に売っている, 目盛り付の物差しで十分である) とコンパスを用いると, 角は容易に三等分される。 これは, アルキメデスによる方法であるそうである。
先ず, 与えられた角は, 鋭角であるとして良い。 何故かというと, 直角は三等分である 30 度が作図できるから問題はない。 鈍角は補角 (= 平角から引いた角) を三等分して, それから 60 度の角を作図すればよい。 又 180 度を超える角度に関しては, その劣角 (つまり 360 度から引いた角) を三等分して, 120 度の角を作図すれば良いからである。
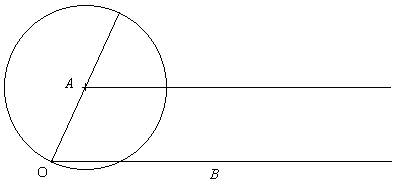
今与えられた (鋭) 角を AOB としよう。 ここで OA は初めに与えられた物差しに付いている二箇所の印の長さにとる。 そして点 A から OB に平行な線を引く。
A を中心として, 半径 OA の円を描く。

先に A から引いた平行線上に点 C をとり, OC との交点を D とするとき, CD が OA と等しい長さになるようにする --- ここで二箇所に印の付いている物差しを使う。
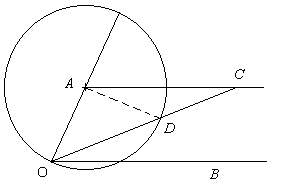
このとき OA = AD = DC であるから,
∠ACD = ∠CAD, ∠ADO = ∠AOD.
明らかに ∠AOD = ∠ADO = ∠ACD + ∠CAD = 2∠ACD.
一方錯角で ∠BOC = ∠ACO = ∠ACD.
よって ∠AOB = ∠BOC + ∠AOD = ∠ACD + 2∠ACD = 3∠ACD = 3∠BOC.
即ち三等分出来たわけである。
(ここの部分が Shochandas 氏の site 「私的数学塾」 の 「作図問題における円の役割」 に link されている。 Wednesday, 24th March, 2004.)
特殊な道具を使うやり方も知られている。 例えばここを参照のこと (ほぼ同じ内容は, 英文であるが Origami Trisection of an angle でも見られる)。 こんな page もある。
これよりも尚複雑な方法を考案する人もいる。 例えば manganetwork 氏の site とか。
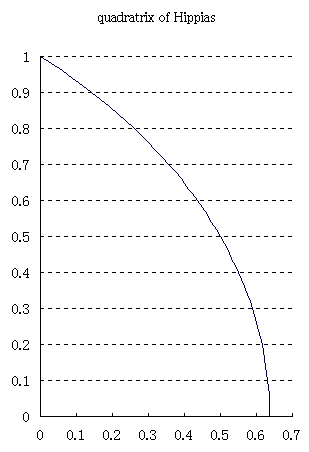
又 quadratrix of Hippias (ヒッピアスの曲線) を用いると, 角を何等分でもできる。
そうする為には, 座標平面上に, 一般角として角を作図しておき, 曲線上の点の y 座標が, 成す角 θ に比例するようにして置けばよい。 比例定数は 2/π にしておけば, 直角のとき y = 1, θ = 0 の時には y = 0 となるので良いであろう。即ち y = 2θ/π.
逆に言うと θ = πy/2 である。 従って y/x = tan θ = tan(πy/2).
即ち x = y/tan(πy/2) = y cot(πy/2). これが quadratrix of Hippias である。
角を n 等分したければ, その角とこの曲線との交点から y 軸に垂線を下ろし, その点と原点との n 等分点から再び x 軸に平行に直線を描き, ヒッピアスの曲線との交点と原点とを結べば, n 等分角が得られるわけである。
近似解法としては, 例えば図のようなものがある。
click すると拡大図が出ます
先ず B から OA と平行な線を引く。 次に OA に等しく AC, CD を採り, C を中心にして半径 CD の円を描き, 前に引いておいた平行線との交点 E を求める。 次に E から OD に垂線 EF を降ろし, O を中心とする OF の弧 FT を描く。すると OT が求める近似三等分線である。
ここに link が貼られていることを発見 ! 私の page も国際的になったなぁ (笑) (ここにも no. 20)。
Wednesday, 3rd July, 2002.
私の所にもついに trisector がやって来たので, その記録♪
岩波数学辞典第 3 版, 136 作図問題
E. Artin, Galoissche Theorie, Teubner, 1959, 邦訳, アルティン
ガロア理論入門, 寺田文行訳, 東京図書, 1974.
Underwood Dudley, What To Do When the Trisector Comes, the Mathematical
Intelligencer, vol. 5, no. 1, 1983, Springer-Verlag, (野崎昭弘訳, 3
等分家がやってきた --- さてどうするか, 数学セミナー (11),
1983, 日本評論社)。
The
Trisection of an Angle.
Angle Trisection.