Archimedes の方法 2

Archimedes が純粋に幾何学的な方法によって, 球の表面積と体積を求めた時, 彼は意外なことに表面積を最初に求めたのである。表面積を最初に求めればよいと分かれば, やるべき道は一つに決まっている (というか他にあまり良い方法がない)。やるのは「林檎の皮むき」と私が呼んでいる方法である。要するに, 球の表面を円錐側面の一部をつなぎ合わせたもので近似していくのである。これは丁度円周の長さを求める時に, 内/外接多角形で近似していくのに似ている (つまりそれを回転させたわけだ)。

証明は普通「球と円柱について」第一巻と呼ばれる「ドシテウスへの手紙」に書かれている。基本的な補助定理 (lemmata) は次の 4 つである。

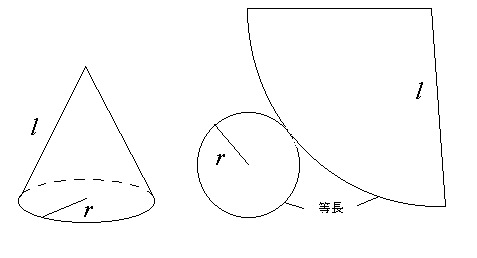
命題 14:
任意の直円錐 (原文: 等脚円錐) の側面積 (原文: 底面を除いた表面) は, その半径が円錐の母線と, 円錐の底面の円の半径との比例中項になるような円の面積に等しい。

命題 15:
任意の直円錐の側面積の底面積に対する比は, 円錐の母線の底面の半径に対する比に等しい。

命題 16:
任意の円錐台に於いてその側面積は, 円錐台の (側面の) 母線長と上下両底面の半径の和の比例中項を半径に持つ円の面積に等しい。

命題 21:
一つの円に正 (2n) 角形 A₀A₁...A_n-1A_nA'_n-1...A'₁ を内接させると,
∑_k=1^n-1A_kA'_k / A₀A_n = A_nA₁ / A₀A₁. (この命題は式を見ただけでは意味がわからないはずである。)

ここまでの証明を書く。

[命題 14 の証明]

述べ方が古代流で分かりにくいが, 円錐の母線長を l, 底面の半径を r, 求める円の半径を R とすれば R² = lr ということである。

扇形の面積が中心角, 従て縁故の長さに比例していること, 又, 円の面積が半径の自乗に比例していることを用いれば簡単で, 側面積が
S = πl² × 2πr/2πl = πrl.
故 R² = lr.

[命題 15 の証明]

上記と同じ記号を用いて,
(πR²) : (πr²) = R² : r² = lr : r² = l : r.

[命題 16 の証明]

述べ方が回りくどいのだが, 円錐台の上/下底面の半径を各々 r₁, r₂, 側面の母線長を lとすると, 側面積が π(r₁ + r₂)l になると述べているだけである。

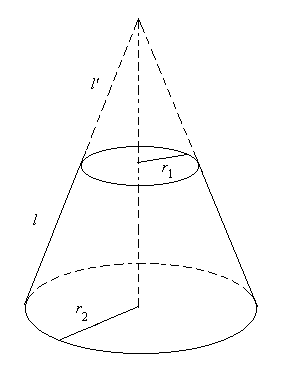
図から, 相似な直角三角形を想像していただいて (或いは 命題 15) から
l' : (l' + l) = r₁ : r₂.
∴(r₂ - r₁)l' = lr₁.
∴l' = (r₁ /(r₂ - r₁))l.
よって 命題 14 から側面積 S について
S = πR₂² - πR₁² = πl'r₁ - π(l + l')r₂ = π((r₁² /(r₂ - r₁))l - (r₂² /(r₂ - r₁))l)
= π(r₁ + r₂)l.

[命題 21 の証明]

命題の式はやたら難しいのだが,

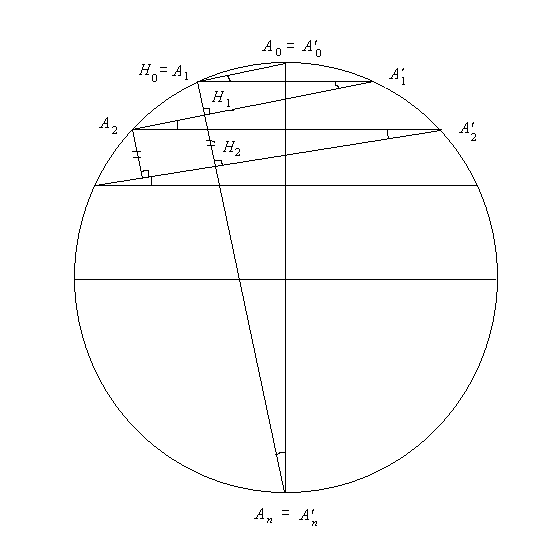
円周角定理より∠A₀A_nA₁ = ∠A₁A'₁A₂ = &c.
従って相似形なので A₀A_n : A_kA'_k = A₀A₁ : H_k-1H_k.
よって A_kA'_k / A₀A_n = H_k-1H_k / A₀A₁ でしかも ∑_k=1^n-1H_k-1H_k = A_nA₁ より言える。

この式は ∠A₀A_nA₁ = π/2n, A,_kA'_k / A₀A_n = sin (πk/n), A_nA₁ / A₀A₁ = cot (π/2n) であることに気付けば実は ∑_k=1^n-1 sin (πk/n) = cot (π/2n), 言い換えると sin (π/2n)∑_k=1^n-1 sin (πk/n) = cos (π/2n) を幾何学的に証明しているのだということが分かる。これが良く積を和に変える公式によって「将棋倒し」で証明されることを知っている人は多いであろう。その公式はこんなところにその源流があったのである。

閑話休題。
次の命題が証明の核心である。
命題 24:
球に正 (2n) 角形の一つの直径 A₀A_n を軸として回転させた回転体を内接させる。この時, この立体の表面積は
πA₀A₁∑_k=1^n-1A_kA'_k  
に等しい。

証明:
命題 14 及び 16 により
S = πA₀A₁(A₁A'₁/2) + ∑_k=1^n-2 π((A_kA'_k/2) + (A_k+1A'_k+1/2))A₁A₂ + πA_n-1A_n
= πA₀A₁((A₁A'₁/2) + ∑_k=1^n-2 (A_kA'_k/2) + ∑_k=2^n-1 (A_kA'_k/2) + (A_n-1A'_n-1/2))
= πA₀A₁(A₁A'₁ + ∑_k=2^n-2 A_kA'_k + A_n-1A'_n-1)
= πA₀A₁∑_k=1^n-1 A_kA'_k.

この先は所謂取り尽くし法 (exhaustion method) を用いるのである。現代なら上記の cos で書いた式を用いて n→∞ などと安易にやるところであるが。

命題 25:
命題 24 の図形の表面積は球の大円の面積 S_g の 4 倍より小さい。

証明:
球の半径を r とすると A_nA₁ < A₀A_n = 2r より, 命題 21 によって
S = πA₀A₁(A_nA₁ / A₀A₁)A₀A_n = πA_nA₁×A₀A_n ＜ π(A₀A_n)² = 4πr² = 4S_g.

次の二つは同様にして示される。

命題 29:
球の周りに命題 24 のような図形を外接させるとその表面積は
πA₀A₁∑_k=1^n-1A_kA'_k
に等しい。

命題 30:
球の周りに外接された図形の表面は, 球の大円の面積 S_g の 4 倍より大きい。

こうしてやっと表面積を得る。

命題 33: [主定理 1]
任意の球の表面積は, それの大円の 4 倍である。

この次に体積の公式を述べる。長くなったので, file を分割することにする。

参考文献:
世界の名著 第 9 巻 ギリシャの科学, アルキメデスの科学 (三田博雄訳) 中央公論社
佐藤徹, アルキメデス方法, 東海大学古典叢書, 1990.

前へ
次へ
球の目次へ
Miscellaneous の index へ
HOME