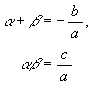
正 17 角形の作図可能性の証明中で用いた幾つかの定理の証明をしておく。
[半角の公式]
三角函数の加法公式のうち余弦の加法公式
cos(α + β) = cos α cos β - sin α sin β
に於いて, α = β = θ と置くと
cos 2θ = cos2 θ - sin2 θ
となるが, ここで 「三平方の定理」 sin2θ + cos2 θ = 1
を用いると, 先ず
cos 2θ = cos2 θ - (1 - cos2θ) = 2cos2θ - 1.
これを解いて
cos2θ = (1 + cos 2θ)/2.
通常これを cos2(θ/2) = (1 + cos θ)/2 の形で書いて, 半角の公式 (power reduction formula) という (half-angle formula というのはこれの平方根 (左辺には絶対値をつけたもの) を言ううらしい)。
同様に sin2(θ/2) = (1 - cos θ)/2 を得る。
辺々割り算して tan2(θ/2) = (1 - cos θ)/(1 + cos θ) を得る。
x に関する二次方程式 ax2 + bx + c = 0 に於いて, その解が α, β であるとしよう。 解としてα, β を持つような最も簡単な x に関する二次方程式は言うまでもなく
(x - α)(x - β) = 0
である。 この方程式を展開して x に関する同類項で纏めれば
x2 - (α + β)x +αβ = 0
である。 これを最初の方程式と比較すると, 二次の係数が明らかに違うので, そこだけをあわせる為に a を両辺に掛けると
ax2 - a(α + β)x +aαβ = 0 …… (1).
即ち今次の定理が得られた。
定理
x に関する二次方程式 ax2 + bx + c = 0 に於いて,
その解が α, β であるとすれば
ax2 + bx + c = a(x - α)(x - β).
さて, 再び最初の式と式 (1) とを比較すると
- a(α + β) = b,
aαβ = c
でなければならない。即ち次の定理を得る。
定理 [二次方程式の解と係数の関係]
x に関する二次方程式 ax2 + bx + c = 0 に於いて,
その解が α, β であるとすれば
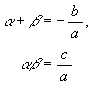
勿論三次以上の方程式に関しても最初の定理と同様の結果, 及び解と係数の関係というものが存在する。
中学では二次方程式の解の公式を扱わなくなるようなので, 念のためにここに書いておく。
x に関する二次方程式 ax2 + bx + c = 0 を monic な (即ち最高次の係数が 1 である) 方程式にする為に, 両辺を a で割る (二次方程式だから二次の係数 a は 0 ではない)
![]()
ここで乗法公式
(x + y)2 = x2 + 2xy + y2
を思い出してもらって先程の方程式を (x + y)2 + z = 0 の形にする。 即ち
![]()
辺々 x の同じ次数の所同士比較すると
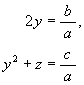
でなければならないことが分かる。即ち
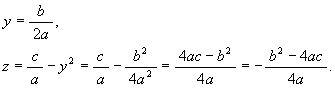
従って,
![]()
移項して平方根を採ると
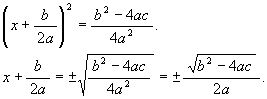
再び移項して
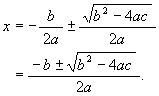
これを二次方程式の解の公式 (根の公式) という。
非常に難しいが三次方程式の解の公式, 四次方程式の解の公式というのも存在する。 しかし五次以上の方程式の一般的な解の公式は存在しない。
[飛ばした式の証明]
2ab = e + f = -1/2,
2ac = 2a + b + d,
2ad = b + c + 2d,
2bc = a + 2c + d,
2bd = a + 2b + c,
2cd = e + f = -1/2.
ここで φ = 2π/17 であり
a = cos φ + cos 4φ,
b = cos 2φ + cos 8φ,
c = cos 3φ + cos 5φ,
d = cos 6φ + cos 7φ
であった。
基本的には積を和に変える公式を用いている。 又 cos nφ = cos (17 - n)φ も用いている。
2ab = 2(cos φ + cos 4φ)(cos 2φ + cos 8φ)
= 2cos φ cos 2φ + 2cos φ cos 8φ + 2cos 4φ cos 2φ + 2cos 4φ cos 8φ
= cos 3φ + cos φ + cos 9φ + cos 7φ + cos 6φ + cos 2φ + cos 12φ + cos 4φ
= cos 3φ + cos φ + cos 8φ + cos 7φ + cos 6φ + cos 2φ + cos 5φ + cos 4φ
= e + f.
2ac = 2(cos φ + cos 4φ)(cos 3φ + cos 5φ)
= 2cos φ cos 3φ + 2cos φ cos 5φ + 2cos 4φ cos 3φ + 2cos 4φ cos 5φ
= cos 4φ + cos 2φ + cos 6φ + cos 4φ + cos 7φ + cos φ + cos 9φ + cos φ
= cos 4φ + cos 2φ + cos 6φ + cos 4φ + cos 7φ + cos φ + cos 8φ + cos φ
= 2(cos φ+ cos 4φ) + cos 2φ + cos 8φ + cos 6φ + cos 7φ
= 2a + b + d.
2ad = 2(cos φ + cos 4φ)(cos 6φ + cos 7φ)
= 2cos φ cos 6φ + 2cos φ cos 7φ + 2cos 4φ cos 6φ + 2cos 4φ cos 7φ
= cos 7φ + cos 5φ + cos 8φ + cos 6φ + cos 10φ + cos 2φ + cos 11φ + cos 3φ
= cos 7φ + cos 5φ + cos 8 φ + cos 6φ + cos 7φ + cos 2φ + cos 6φ + cos 3φ
= cos 2φ + cos 8φ + cos 3φ + cos 5φ + 2(cos 6φ + cos 7 φ)
= b + c + 2d.
2bc = 2(cos 2φ + cos 8φ)(cos 3φ + cos 5φ)
= 2cos 2φ cos 3φ + 2cos 2φ cos 5φ + 2cos 8φ cos 3φ + 2cos 8φ cos 5φ
= cos 5φ + cos φ + cos 7 φ + cos 3φ + cos 11 φ + cos 5φ + cos 13φ + cos 3φ
= cos 5φ + cos φ + cos 7 φ + cos 3φ + cos 6φ + cos 5φ + cos 4φ + cos 3φ
= cos φ + cos 4 φ + 2(cos 3φ + cos 5φ) + cos 6 φ + cos 7φ
= a + 2c + d.
2bd = 2(cos 2φ + cos 8φ)(cos 6φ + cos 7φ)
= 2cos 2φ cos 6φ + 2cos 2φ cos 7φ + 2cos 8φ cos 6φ + 2cos 8φ cos 7φ
= cos 8φ + cos 4 φ + cos 9φ + cos 5φ + cos 14φ + cos 2φ + cos 15φ + cos φ
= cos 8φ + cos 4 φ + cos 8φ + cos 5φ + cos 3φ + cos 2φ + cos 2φ + cos φ
= cos φ + cos 4 φ + 2(cos 2φ + cos 8φ) + cos 3 φ + cos 5φ
= a + 2b + c.
2cd = 2(cos 3φ + cos 5φ)(cos 6φ + cos 7φ)
= 2cos 3φ cos 6φ + 2cos 3φ cos 7φ + 2cos 5φ cos 6φ + 2cos 5φ cos 7φ
= cos 9φ + cos 3φ + cos 10 φ + cos 4 φ + cos 11 φ + cos φ + cos 12φ + cos 2φ
= cos 8φ + cos 3φ + cos 7φ + cos 4 φ + cos 6 φ + cos φ + cos 5φ + cos 2φ
= e + f.