Saturday, 6th July, 2002.
Sunday, 7th July, 2002.
私の角の三等分の page は google で検索すると上位 5 番目に rank されている。 そのおかげかどうか知らないが, ユーゴスラヴィアで報道通訳を本業とされているベオグラード在住の大塚真彦氏 (HP は http://www.pluto.dti.ne.jp/~katu-jun/yugo/) から, Tuesday, 2nd July, 2002 に次のような内容の e-mail が送られて来た。
昨日 30 日付の当地日刊紙ポリティカの日曜版で, 端折りますが要するに当地の小学校の先生が 2500 年来の難問だった角の三等分法を発見してしまった, 本の出版準備はしているし知的所有権に関する特許を取ったし, 先生曰く 「素粒子のミクロから宇宙工学まで役立つ大変な発見なんだ」 云々, で大騒ぎ, という記事が出ました。
記事の詳しい内容はあとで教えてもらったので, 数学的部分のあとに書くとして, 先ずはその描き方を解説しよう。
[スラビッチ教諭の角の三等分法]
更に, スラビッチ教諭によれば類似の方法で 5 等分, 7 等分等も可能 (新聞には示
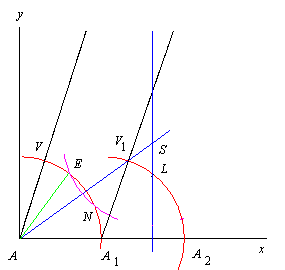
されていません)。 だとのことである。 (下の図は大塚氏の送ってきた図を多少描き変えたもの)

見て分かるようにこれは古典的作図 (即ち目盛りのない定規とコンパスだけを用いて作図するもの) であるから, これで三等分できないということは既に 1837 年に P.-L. Wantzel (ワンツェル) が証明済みなので, 検証するまでもなく, 三等分できるはずがない。 (しかし 5 等分, 7 等分はどうやってやるのだろう, L を出すときに 3/4 の代わりに 5/6 とかでやるのだろうか ?)
誤差を調べてみよう。
図のように x 軸と y 軸を導入 (A = O 即ち原点と) し, 上記で描いている円の半径 (即ち R) は全て 1 としよう。 又, 与えられた角の大きさを θ としよう。
A1(1, 0), A2(2, 0) である。
描き方から V1 (1 + cos θ, sin θ), L(1 + cos (3θ/4), sin (3θ/4)) がすぐ分かる。
直線 AV1 は y = (sin θ/(1 + cos θ))x (= x tan(θ/2)) だから,
S(1 + cos (3θ/4), sin θ(1 + cos (3θ/4))/(1 + cos θ))
であることが分かる。
S 中心, 半径 1 の円の方程式は
(x - (1 + cos (3θ/4)))2 + (y - sin θ(1 + cos (3θ/4))/(1 + cos θ))2
= 1
で, 最初の円 x2 + y2 = 1 と連立させると
(1 + cos θ)x + sin θ y = 1 + cos (3θ/4)
が成り立つので, 最初の円の方程式から sin2 θ x2 + sin2 θ y2
= sin2 θ としておいて代入すると
2(1 + cosθ)x2 - 2(1 + cosθ)(1 + cos (3θ/4))x + (1 + cos (3θ/4))2
- sin2 θ = 0
という方程式を得る。 この方程式を便宜上 ax2 + bx + c = 0, その判別式を D とする。
ここから (この方程式を実際に解くのは簡単だが, 式があまり簡単にならないみたいなので) Microsoft Excel 2002 を用いて計算させると, 次のような表を得る。
| 角度 θ (deg) | rad | a | b | c | D | x | y | y/x | θ/3 [rad] | θ/3 [deg] | 誤差 |
| 3 | 0.05236 | 3.997259 | -7.99144 | 3.994178 | 3.75E-06 | 0.999857 | 0.016925 | 0.016927 | 0.016926 | 0.969763 | 0.030237 |
| 6 | 0.10472 | 3.989044 | -7.96579 | 3.976753 | 5.97E-05 | 0.999427 | 0.033854 | 0.033874 | 0.033861 | 1.940083 | 0.059917 |
| 9 | 0.15708 | 3.975377 | -7.9232 | 3.94785 | 0.000299 | 0.998709 | 0.050794 | 0.050859 | 0.050816 | 2.911523 | 0.088477 |
| 12 | 0.20944 | 3.956295 | -7.86388 | 3.907678 | 0.000932 | 0.997702 | 0.067748 | 0.067904 | 0.0678 | 3.884652 | 0.115348 |
| 15 | 0.261799 | 3.931852 | -7.78815 | 3.856523 | 0.002235 | 0.996405 | 0.084722 | 0.085028 | 0.084824 | 4.860053 | 0.139947 |
| 18 | 0.314159 | 3.902113 | -7.69641 | 3.794752 | 0.004534 | 0.994813 | 0.101722 | 0.102252 | 0.101898 | 5.838325 | 0.161675 |
| 21 | 0.366519 | 3.867161 | -7.58913 | 3.722803 | 0.008184 | 0.992924 | 0.118752 | 0.119598 | 0.119033 | 6.820091 | 0.179909 |
| 24 | 0.418879 | 3.827091 | -7.46687 | 3.641187 | 0.013545 | 0.990734 | 0.135819 | 0.13709 | 0.13624 | 7.805999 | 0.194001 |
| 27 | 0.471239 | 3.782013 | -7.33026 | 3.550478 | 0.020963 | 0.988237 | 0.152929 | 0.15475 | 0.153532 | 8.79673 | 0.20327 |
| 30 | 0.523599 | 3.732051 | -7.18002 | 3.451312 | 0.030738 | 0.985429 | 0.170089 | 0.172604 | 0.17092 | 9.793005 | 0.206995 |
| 33 | 0.575959 | 3.677341 | -7.01689 | 3.344379 | 0.043107 | 0.982302 | 0.187306 | 0.19068 | 0.188419 | 10.79559 | 0.204409 |
| 36 | 0.628319 | 3.618034 | -6.84173 | 3.230414 | 0.05822 | 0.978848 | 0.204587 | 0.209008 | 0.206041 | 11.80531 | 0.194693 |
| 39 | 0.680678 | 3.554292 | -6.6554 | 3.110197 | 0.076121 | 0.97506 | 0.221941 | 0.227617 | 0.223804 | 12.82304 | 0.176964 |
| 42 | 0.733038 | 3.48629 | -6.45884 | 2.98454 | 0.096736 | 0.970927 | 0.239376 | 0.246544 | 0.241723 | 13.84973 | 0.150266 |
| 45 | 0.785398 | 3.414214 | -6.25303 | 2.854281 | 0.119865 | 0.966437 | 0.256904 | 0.265826 | 0.259817 | 14.88644 | 0.11356 |
| 48 | 0.837758 | 3.338261 | -6.03897 | 2.720278 | 0.145176 | 0.961577 | 0.274535 | 0.285505 | 0.278106 | 15.93429 | 0.065706 |
| 51 | 0.890118 | 3.258641 | -5.81771 | 2.583401 | 0.17221 | 0.956333 | 0.292281 | 0.305627 | 0.296611 | 16.99455 | 0.005452 |
| 54 | 0.942478 | 3.175571 | -5.59029 | 2.444521 | 0.200388 | 0.950686 | 0.310155 | 0.326244 | 0.315356 | 18.06859 | -0.06859 |
| 57 | 0.994838 | 3.089278 | -5.3578 | 2.304506 | 0.229027 | 0.944617 | 0.328174 | 0.347414 | 0.334369 | 19.15796 | -0.15796 |
| 60 | 1.047198 | 3 | -5.12132 | 2.164214 | 0.257359 | 0.938104 | 0.346353 | 0.369205 | 0.35368 | 20.26439 | -0.26439 |
| 63 | 1.099557 | 2.907981 | -4.88192 | 2.024479 | 0.28456 | 0.931121 | 0.364711 | 0.391691 | 0.373323 | 21.38982 | -0.38982 |
| 66 | 1.151917 | 2.813473 | -4.64068 | 1.886114 | 0.309772 | 0.923636 | 0.383271 | 0.414959 | 0.393335 | 22.53645 | -0.53645 |
| 69 | 1.204277 | 2.716736 | -4.39865 | 1.749893 | 0.332141 | 0.915615 | 0.402056 | 0.439111 | 0.413762 | 23.7068 | -0.7068 |
| 72 | 1.256637 | 2.618034 | -4.15688 | 1.616554 | 0.350848 | 0.907016 | 0.421095 | 0.464264 | 0.434652 | 24.90375 | -0.90375 |
| 75 | 1.308997 | 2.517638 | -3.91636 | 1.486786 | 0.365141 | 0.897792 | 0.440419 | 0.490558 | 0.456065 | 26.13062 | -1.13062 |
| 78 | 1.361357 | 2.415823 | -3.67809 | 1.361229 | 0.374372 | 0.887885 | 0.460065 | 0.518159 | 0.478069 | 27.39133 | -1.39133 |
| 81 | 1.413717 | 2.312869 | -3.44299 | 1.240465 | 0.37802 | 0.877226 | 0.480077 | 0.547267 | 0.500742 | 28.69043 | -1.69043 |
| 84 | 1.466077 | 2.209057 | -3.21195 | 1.125015 | 0.375724 | 0.865734 | 0.500505 | 0.578128 | 0.524182 | 30.03339 | -2.03339 |
| 87 | 1.518436 | 2.104672 | -2.98581 | 1.015335 | 0.367297 | 0.853307 | 0.521408 | 0.611044 | 0.548501 | 31.42677 | -2.42677 |
| 90 | 1.570796 | 2 | -2.76537 | 0.911813 | 0.352746 | 0.839823 | 0.542861 | 0.646399 | 0.57384 | 32.87859 | -2.87859 |
この表で, 一番左が 3 度毎の角度, 次がそれを弧度法 (radian) に直したもの。 a, b, c, D は上記の方程式のもの, x
はこの方程式から求めた N の x 座標, y は連立方程式から求めた N の y 座標, y/x はそれらの比で, θ/3 は Arctan(y/x)
で求めた, ∠NAA1 (= ∠EAV) の角度である。 誤差は, 真の値から計算値を引いたもの (度数法) である。
Underwood
Dudley 先生に倣って私も表を作成してみた (笑)。 Microsoft Excel の計算誤差がこんなに大きいはずはないので,
かなり誤差が大きいことが分かる。 この作図法が新しいものであるかどうかは不明である。 三等分家達の色々な試みについて興味をお持ちの方は,
Underwood Dudley: The
Trisectors --- formerly entitled A Budget of Trisections, the
Mathematical Association of America,
176pp., paperbound, 1994, ISBN 0-88385-514-3
があるのでご紹介しておく。
Prof. Dudley に直接 contact を取った結果, 次のような comment を頂いた:
女性の三等分家は珍しいこと (通常男だけが愚かでそんなことをする usually only men are so foolish),
上記の構成法は一見して新しいものに見えるが, 調べてみないと良く分からないこと (Sometimes constructions that seem to be
original turn out to be old ones in disguise).
さて, 記事の内容をもう少し詳しく送ってもらったので, それを書いておこう (原文から若干変えた部分がある)。
(件の新聞の) 見出しは 「『不可能』の解決 --- 25 世紀続いた誤解」 と書いてあり, アルキメデス (ユークリッドではなく !) もダヴィンチも解けなかった謎をこのオバサンが解いちまったんだぞ, というような調子の記事だった。 記者はヨヴァン・ニコリッチという人で (こういう記事を書くくらいだから) 多分数学は素人であろう。
新聞の詳細はポリティカ紙が 「マガジン」 という名で出している日曜版綴じ込み付録 (2002 年 6 月 30 日号) で, 他は旅行とか料理とか, ちょっと大衆的な性格の記事が多いもので, 記事としても一寸怪しげ。
先生のフルネームはスロボダンカ・スラヴィッチ (Slobodanka Slavic), 写真を (大塚氏が) 見る限り冴えない普通のオバサンちゅう感じです。 ベオグラード市内にある 「国際連合」 小学校の算数 / 数学・理科 / 物理の教諭 (当地は小学校は 8 年制で, 6 年生ぐらいからかなり科目が細分化されます)。 本人曰く, ユーゴ (セルビア東部) にある考古遺跡レペンスキ・ヴィールの住居を分析した図面 --- どんな図面なんだろう ? --- を見ていてピンと来た, とのこと。 というわけでニコリッチ記者の記事も全体としては 「どうだレペンスキ・ヴィールだぞ, 素粒子から宇宙工学まで役立つ 25 世紀の謎をセルビア人が解いちまったぞ, オレたちセルビア人はスゲエだろう」 みたいなトーンが (外国人の私には) 言外に感じられる 「大衆的な」 ものに仕上がっていました。
とのことであった。
今回のことがあって, 件の Dudley 先生の What To Do When the Trisector Comes, the Mathematical Intelligencer, vol. 5, no. 1, 1983, Springer-Verlag, (野崎昭弘訳, 3 等分家がやってきた --- さてどうするか, 数学セミナー (11), 1983, 日本評論社) を引っ張り出して懐かしく読ませてもらったところ,
三等分家の目だった特徴は, 皆年寄りだということである, 典型的な三等分家は, 幾何の授業で角の三等分のことを聞いて, 何年も経ってから, 大抵定年退職の後にやっと彼の方法を見つけるのである。 「彼の」 と言ったのは, 別に男女差別主義からではなく, 殆ど統べての三等分家が男だからである。私が知っている女性の三等分家は二人だけで, いい加減な統計処理によれば, 女性の三等分家は 4 % 以下であることが 95 % の信頼度で言える。 女性はそんなことに時間を無駄にするほど愚かではない。
との記述を発見。 仮に 1983 年以来女性の三等分家が発見されなかったとしたら, 彼女は三人目ということになる。 又同じ記事で
三等分家達は, 角の三等分が重要であると考えている。 分度器で素早く十分な仕事ができるとは, 誰からも教わらなかったのであろう。 分度器がなくても, 二ヶ所に印をつけた Archimedes の定規があれば良い。 (中略) 私が見た, 三等分の最も並外れた応用は, 1934 に示唆された。
... ... 角の三等分は, おそらくは現代の賢者の石の発見への鍵であることが明らかにされるであろう。賢者の石によって, ある物質を他のものに変えること --- 即ち, 実用的錬金術が可能になるのである。
(中略) 三等分家は普通自分達の方式を著作権で保護し, 登録し, 証人を用意している。
女性で現役の教師というところを除けばぴったりではないか ! (笑)
これの誤差を計算していて結構楽しい思いをさせてもらったが, 今回は間接的な問い合わせだから良かったようなものの, 三等分家本人が何人も来たらさすがに大変である。 本人が来ないことを祈ろう (笑)。
大塚氏の HP http://www.pluto.dti.ne.jp/~katu-jun/yugo/。
大塚氏に教えてもらったボスニア語 (セルビアクロアチア語) のとっても怪しい, 三等分家 カラチ・アダモフ=ルジュディヤ (Kalač Ademov Ruždija) の site.
戻る
Miscellaneous の index へ
HOME