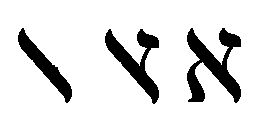
某宗教団体の新しい名前でもあるが, 本来はヘブライ文字の第一文字の名前。 (Symbol の中と Times New Roman のラテン拡張文字 B の中にはあるのだが 出るかな ? 因みに上記は Symbol) 書き方は難しいが, ヘブライ語は右から左へ書くということを念頭において書くと良い。
アレフというのはヘブライ語で「牛」の意味。 フェニキア文字の第一文字から発生したと考えられており, それは今日の A を左に 90 度回転させたような形をしている。
数学ではこれを集合の濃度 (potency, power, 又は基数, cardinal number, cardinality) の記号として用いている。 最初に使ったのは Georg Cantor (ゲオルク・カントル, デンマーク人) である。 その後ヘブライ文字は一般的には使われていないので, これが唯一の数学に現れるヘブライ文字と思って良い。
と書いたところ, 北見工業大学で数理論理学 (特に集合論) を研究されておられる渕野昌先生から, 次のようなご指摘を mail で頂いた。
ヘブライ文字の第二文字 beth ב と第三文字 gimmel ג も集合論では濃度を表す記号として良く用いられるそうである (専門外なので知らなかった)。 これに関して後述する。
濃度というのは集合の要素の個数の拡張である。 数というものをまったく知らないとして, 例えば蜜柑 が 3 個あり, 林檎が 3 個あるとき それらが同じ数であるというのをどうやって知るのだろうか ?
数学者達が用意した答えが 「それらを線で結ぶ」 ということである。 一つのものから一本しか線が出ないようにして, ものとものとを結んでいくとき (有限の数の場合) それらが丁度余りなく結ばれれば数が等しく, そうでなければ線が余った側が数が多いということになる。 数学では 「丁度余りなく結ばれる」 場合上への一対一対応が付くという。
無限個の要素を持つ集合について同じことを考えると, 一番「小さい」無限の数 (= 濃度) は 自然数 (正の整数 1, 2, 3, 4, ... の全部) の集合の濃度でそれを À0 という記号で表す。 (そしてアレフゼロと読む)
実は, 整数 (自然数に 0 と負の整数 -1, -2, -3, ... を加えたもの) も自然数と同じ濃度であり有理数 (整数分の整数という形をした分数全体) も自然数と同じ濃度であることが証明できる。
ところが実数 (数直線上にのっている数の総て) は Cantor が 「対角線論法 diagonal method」 という 有名な方法を用いて自然数の集合の濃度よりは大きいことを示した。 この濃度を À という記号で表す。
Cantor はこれを À1 という記号で 表したかった (連続体仮説 continuum hypothesis) が, 自然数の濃度と実数の濃度の間には別の濃度がないということが証明出来なかったので, 今日でもこれを À という記号で表しているのである。
さて, 実は上記の連続体仮説は, ZFC という集合論の基礎となっている公理 (定義みたいなもの) からは決して証明出来ないし, それが正しくないということも証明できない ということが Cohen によって証明されている。
さて実は, この À という記号を使い始めたのは, Georg Cantor であると書いたが, 「集合の濃度の記号として」 用いたのはその通りであるが, この文字を数学記号として用いたのは実は Wronski (ロンスキ, Höené Joseph Maria, 1778--1853) だそうである。 Cantor が 3rd March, 1845--1st June, 1918 であることを考えれば, 明らかに Wronski の方が先である。 彼はこの記号を対称化する記号 (特に À 函数は完全斉次対称式) として用いているのだそうである。 彼は他のヘブライ文字も使用しているそうである。 (本段落は Z to A 氏による「数学セミナー」(5), 2000, p. 7 による。) しかし現在ではその意味で使う人は誰もいない。
書き順であるがイスラエルの小学校の教科書によれば次の通りだそうである。
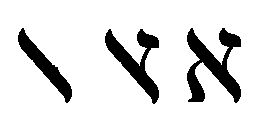
これは関沢正躬(東京学芸大学教養学部, 「数学セミナー」(5), 2000, p. 50, 特集: 現代を生きるための数学「記号」) によった。 まさか三画の文字であるとは思わなかった (!)。
数学科の学生になると, 大抵この aleph という文字をどう書いたらいいのかという問題が起こる。 私も長らく疑問だったが, ヘブライ語の初歩みたいな本が存在するので, それを見てみたところ, 英語の block 体のような文字が存在して
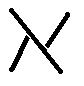
の様に書くのだそうである (一画一画離して書くらしい)。 書き順は上のものと同じ。 因みに筆記体も存在して, /c の様に書く。 これはヘブライ語が右から左に書くのに対応して, c の方から書くのである。
よく考えると, 普通に数学に出て来る文字の書き方を誰も知らないというのは問題で, (日本はともかく) そこら中にユダヤ人がいるのだから, どうしてユダヤ人に書き方を訊かないのかとても不思議であるし, ヘブライ語の書き方が出ている本があるのだから, 誰も参照しないというのは, いわば教員の怠慢である。
因みに, ギリシャ文字の方も, 手書きで書くときに, 書き順などが良く問題になるが, これもギリシャ語の初歩の本を当たってみると良い。β, θ, σ, μ 等はギリシャ人の書いているものが, 普通の数学者が書いている文字と書き順が違う (ばかりか, β, θ 等は見た目も違う) ので, 衝撃を受ける。
Thursday, 30th May, 2002.
北見工業大学の渕野昌先生からは, 記号 À は À0, À1, À2, ... と 基数の順 (集合の大きさの順) に増えていくのであるが, ב (beth) は (ヘブライ文字の特性で Times New Roman では subscript を右につけることがどうしても出来なかったので, 右に subscript が付いていると思って) 添字が 1, 2, ... と増えるに従って, 冪集合の濃度で増えていくのだ, ということを教えていただいた。 又 ג (gimmel) は見える人には分かるであろうが, λ に見えるので, λ で代用することもあるかもしれないそうである。 実は Cantor の原論文にはこれらのヘブライ文字 (実はこれの次のヘブライ文字 ד ה 等) も使われていたのだが, 今も使われているとは思わなかったので, 無視したのであった。
又, ユダヤ系のスイス人の数学者に 「つながってハーケンクロイツと位相同型にならないように書いてほしい」 と言われたことがあったそうである。 多分そのように書く人々が沢山いるのであろう。 --- 思い出してみると, 私も二画でくっつけて書いていたのでハーケンクロイツと位相同型だった (^_^; 尚, 活字の方は払いがたまたまくっついて見えるだけらしい。
更に Joge Luis Borges (ボルヘス) には El Aleph という小説があるということである。 USA の Yahoo ! で検索して, 英語訳を link しておいた。
http://ore.to/~box/0/Out/borges.html と 1978年発行・集英社 「世界文学全集」 9 巻「ボルヘス集・篠田一士訳/伝奇集/エル・アレフ/汚辱の世界史」 等という日本語訳があることも見つけた。
Thursday, 4th July, 2002.
この page が西岡昌紀氏の発行する mail magazine 「さくら通信」 第 100 号 (Monday, 12th November, 2001) に掲載されました。
それによれば, この文字は元はエジプト文字であること, この形が, 「百という数を聞いてびっくりしている人の形」 によるということです。
又この mail によって 009 氏の page に対角線論法が出ていたので紹介する。 但し, 残念なことに, この page では無限は 「可算濃度」 と 「連続濃度」 しかないと断言しているが, それは誤りで, 無限にも無限の段階があるのである。
ここも渕野先生にご指摘をいただいた。 「無限にも無限の段階」 の 「無限」 は加算無限ではなくて class many --- は日本語訳出来ないぞ (^_^;; --- である。 うん, 確かに。 「全ての濃度の集合」 というのを考えると, 集合論的矛盾が生じるというのは以前から分かっていたことであった。
この page は喜多ロー氏の World Scissors に link されている。(Saturday, 20th March, 2004)
ハンバーグ専門店 「びっくりドンキー」 の会社も 「アレフ」 らしい。
Saturday, 4th February, 2006.
渕野昌先生の HP.
嘉田勝: 公理的集合論ってなぁに ? (What is Axiomatic Set Theory ?)