数学用語としての T3 は普通 T 3と書かれるがこの T は torus (トーラス, 複数形 tori, トーライ) の略である。普通の英語としては建築用語でトールスという柱の一部を指すものであるらしい (綴りは一緒) 。 一般にはT nでこのn は次元を表しており, n 次元トーラス (n-torus) という。
いきなりT 3では難しいので先ずT 2から。
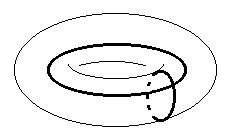
二次元トーラスはものすごく簡単に言うと普通のドーナツ
或いは浮き輪の
(表面の) 形である。この形には二種類の円が関係している。(下図,
尚, これらの円を各々この torus の基本 cycle という)

この図から, torus というものは小さな円を大きな円に沿って「回転」させたものだということがお分かりいただけるだろうか。 この意味で, T 2 = S 1×S 1 (直積空間) という風に表現されている。但しS 1は円である。
この話を一次元上げたものが三次元トーラスT 3であるが, この「一次元上げる」というのがとんでもなく難しいことは私も良く知っているので, 一寸説明する。
先ず事実としてT 3 = S 1×S 1×S 1 =T 2×S 1 である。想像をたくましくしてもらって, 我々の住んでいる世界より一次元高い世界 (それは 4 次元と思うかもしれないが Einstein (アインシュタイン) にしたがって 5 次元である。余計な一次元は「時間」) で, 上記の図のT 2をあさっての方向に向けて描いてある円S 1に沿って「回転」させる。 こうして得られたのが目標のT 3 。想像できた ? (説明になってない ?)
尚, この説明で数学の専門家というのは, 次元の高い世界も見えていてすごいなぁと思ったりするかもしれないが, 実はそういう人は稀である。多くの人は「見えない」。見えている気になっているか, 見えてないが取りあえず計算が出来たりするか, その程度である。見えるか見えないかということに関しては, みんな普通の人間。時々, 高次元の世界が見えるという人がいるが, その多くが生まれつき目の見えない人であるのは何故なのか良く分かっていない (しかも本当に見えているらしい)。