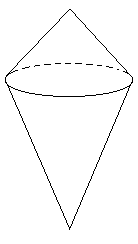
Archimedes の方法 2(承前)

Archimedes の球の体積の公式は, あくまでも 「その球の大円に等しい底面とその半径に等しい高さとを持つ円錐の体積の 4 倍になる。」 というものであるから, 前述の方法から直ちに体積が求まるというわけにはいかない。円錐台の体積の和を, 一つの円錐に等積であることを述べなくてはならないわけである。

定義 6:
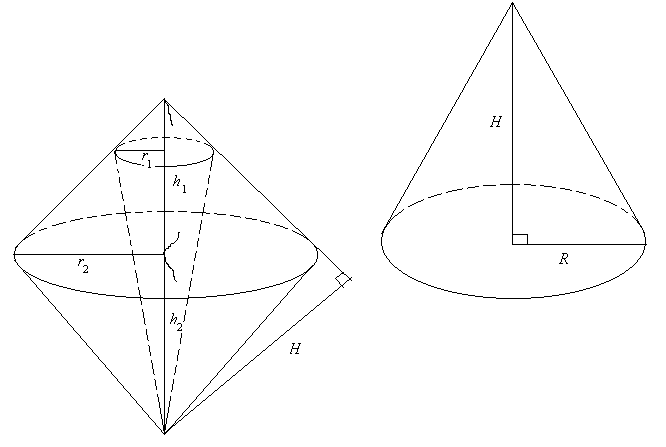
私 [= Archimedes] が立体偏菱形 (へんりょうけい) と呼ぶものは, 同じ底面積を持つ二つの円錐がそれらの頂点を底の平面に関して別々の側に持ち, それらの軸が一直線上に横たわるような位置にあるとき, 両方の円を結合した立体図形のことである。

命題 17:
もし二つの直円錐が与えられていて, 一方の円錐の側面積が他方の円錐の底面に等しく, 前者の底面の中心からその円錐の母線 (の一つ) に引いた垂線が, 後者の高さに等しいならば, 両円錐 (の体積) は等しい。

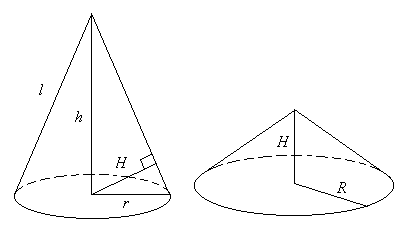
証明:
図で相似であるから r : H = l : h. ∴l = hr / H.
従って 命題 14 と仮定とから
πR² = π(hr / H)r.
∴HR² = hr².
∴πHR² /3 = πhr² /3.

命題 18:
二つの直円錐からなる任意の立体偏菱形は, 次のような円錐と等積である: その底面が立体偏菱形の第一の円錐の側面積に等しく, その高さが第二の円錐の頂点から第一の円錐の (一つの) 母線に引いた垂線に等しい。

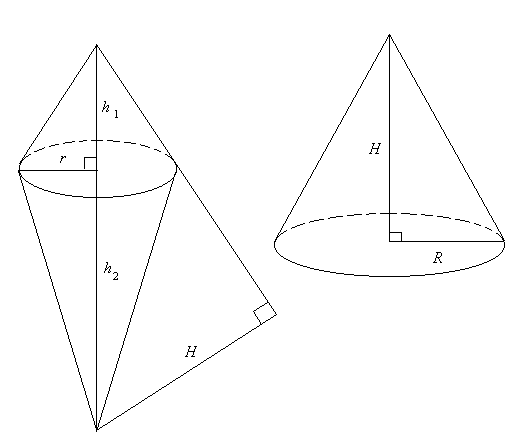
証明:
相似を用いて, 図より
r : (r² + h₁²)^1/2 = H : (h₁ + h₂).
∴H = r(h₁ + h₂)/(r² + h₁²)^1/2.
又 命題 14 より πR² = π(r² + h₁²)^1/2r. よって
πR²H /3 = π(r² + h₁²)^1/2r ( r(h₁ + h₂)/(r² + h₁²)^1/2) /3 = πr²(h₁ + h₂) /3.

命題 19:
もしも直円錐をその底面に平行な一平面によって切り, こうして出来た円上に底面の中心を頂点とする円錐を描き, こうして出来る立体偏菱形を円錐全体から引き去るならば, 周りに残った部分は, 次の円錐と等積である: 底面が平行な二平面の間にある円錐台の側面積に等しく, その高さが底面の中心から円錐の一つの母線に引いた垂線に等しいような円錐に等しい。

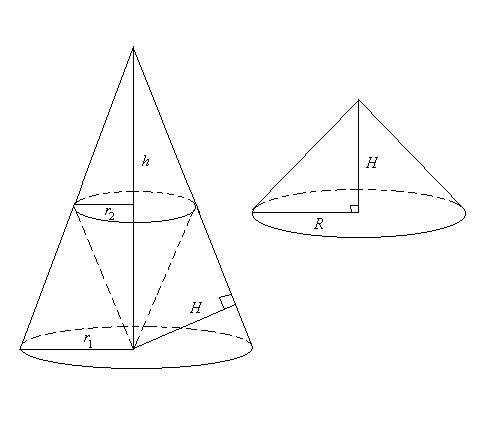
証明:
図で相似と 命題 16 とから,
πR² = π(r₁ + r₂)×(r₁ - r₂)/r₁×(r₁² + h²)^1/2
= π(r₁² - r₂²)/r₁×(r₁² + h²)^1/2.
又, 相似より H = (r₁/(r₁² + h²)^1/2)h.
よって
πR²H /3 = π(r₁ + r₂)×(r₁ - r₂)/r₁×(r₁² + h²)^1/2×(r₁/(r₁² + h²)^1/2)h /3
= π(r₁² - r₂²)h /3.

命題 20:
もしも二つの直円錐からなる一つの立体偏菱形の第一の円錐を底面に平行な一平面によって切り, こうして出来た切り口の円上に第二の円錐と同じ頂点を持つ一つの円錐を描き, こうしてできる立体偏菱形を (最初の) 立体偏菱形から引き去るならば, 周りに残る部分は次の円錐と等積である: その底面が平行な二平面の間にある円錐台側面積に等しく, その高さが第二の円錐の頂点から第一の円錐の (一つの) 母線に引いた垂線に等しい。

証明:
命題 18 及び 19 でのようにして
πR² = π(r₁² - r₂²)/r₁×(r₁² + h²)^1/2. H = (r₁/(r₁² + h²)^1/2)(h₁ + h₂)
より
πR²H /3 = π(r₁² - r₂²)/r₁×(r₁² + h²)^1/2×(r₁/(r₁² + h²)^1/2)(h₁ + h₂) /3
= π(r₁² - r₂²)(h₁ + h₂) /3.

以上の命題から

命題 26:
球に内接された 命題 24 でのような正 (4n) 角形の回転体の体積は次の円錐と等積: 底面の円がその回転体の表面積に等しく, その高さが球の中心から (元の) 多角形の一辺に引かれた垂線に等しい。

これと命題 25 とから次の命題を得る。

命題 27:
上述の回転体の体積は次の円錐の体積の 4 倍より小さい: 底面積が球の大円に等しく, その高さが球の半径に等しい。

同様にして

命題 31:
球に外接された 命題 29 のような正 (4n) 角形の回転体の体積は, 底面積がこの回転体の表面積に等しく高さがこの球の半径に等しい円錐の体積に等しい。

系:
上述の回転体の体積は, 底面積が球の大円の面積に等しくその高さが球の半径に等しい円錐の体積の 4 倍より大きい。

こうして取り尽くし法によって次の命題を得る。

命題 34: [主定理 2]
任意の球 (の体積) は, 底面積が球の大円の面積に等しくその高さが球の半径に等しい円錐の体積の 4 倍である。

命題 33 と 命題 34 とから次の系を得る。

系:
底面が球の大円で高さが球の直径に等しい任意の円柱は, (体積が) 球の 1 + 1/2 = 3/2 倍である。

参考文献:
世界の名著 第 9 巻 ギリシャの科学, アルキメデスの科学 (三田博雄訳) 中央公論社
佐藤徹, アルキメデス方法, 東海大学古典叢書, 1990.

前へ
次へ
球の目次へ
Miscellaneous の index へ
HOME