Thursday, 18th May, 2000.
上記の求積法は実に巧妙で, 古代にあっては Archimedes を待ってはじめてできたであろう。(中略) 然るに 18 世紀には, このような求積問題は, 次のような一般的の方法によって何人にも容易に解かれたであろう。 高木貞治, 解析概論 第三章 §29 微分法以後の求積法
上記の高木の言葉は放物線とその割線とで囲まれた図形の面積を求める問題に関して言われたものであるが, 以上見てきたように球の表面積および体積に関しても充分当てはまるものとなっている。
まず初めに体積の方からやってみよう。

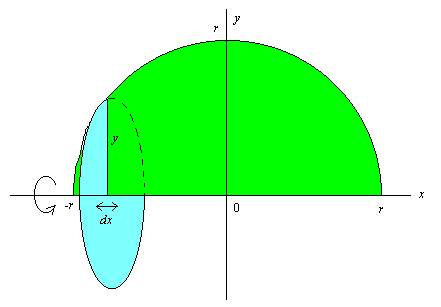
球というのは回転体であるから, 図で, y
部分を回転させた円の面積に微細な厚み dx
を掛け算したものを -r から r 迄足し合わせる,
というのが超準解析的説明である。円の方程式が x2
+ y2 = r2 である。明らかに左右対称だから,
0 から r までの積分にして,
あとで二倍しても同じであるから,
V = 2∫0rπy2dx = 2π∫0r(r2
- x2)dx = 2π[r2x - x3/3]0r
= 2π(r3 - r3/3) = 4πr3/3
と非常に簡単に出る。
表面積の方は多少工夫がいる。というか回転体の表面積の公式はあまり知られていないので, ここで作り方も説明しておく。
基本となっているのは, Archimedes の方法 2 で述べた命題 16 である。(偉大なる Archimedes !) もう一度述べておくと, 円錐台の側面積は, 円錐台の上/下底面の半径を各々 r1, r2, 側面の母線長を l とすると, 側面積が π(r1 + r2)l になるということである。
この式をもう一度見直していただいて 2π×(r1 + r2)/2×l と思い直すと, 円錐台の側面は, 「母線の中央の描く長さ 掛ける 母線の長さ」であることが容易に見て取れるであろう。(このことはもっと一般の形で成り立つが, それは微分幾何の問題だからここには書かない)
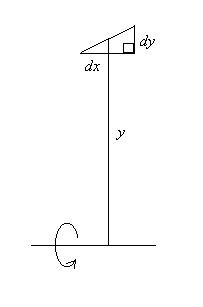
ここまでを前提とすると, 図に見られるように,
回転体の表面積は母線の線素の描く部分の面積を足し合わせたものである。
線素の長さが ds = (dx2 + dy2)1/2 であるというところは,
解析の基礎のところで学んでいるはずである。(とはいえ,
今では大学に行かなければ習わないことになってしまったが)
従って回転体の母線が x の函数 y であり, 回転の中心が x
軸である場合には, 回転体の表面積の公式は
S = 2π∫abyds = 2π∫aby(dx2 + dy2)1/2
= 2π∫aby(1 + (dy/dx)2)1/2dx
となるわけである。
この公式を用いると, 球の場合 y = (r2
- x2)1/2 だから dy/dx = -2x(r2
- x2)-1/2/2 = -x(r2
- x2)-1/2 である。従って (また対称性を使って)
S = 2π∫-rr(r2
- x2)1/2(1 + (-x(r2
- x2)-1/2)2)1/2dx
= 4π∫0r(r2
- x2)1/2(1 + x2/(r2
- x2))1/2dx
= 4π∫0r(r2
- x2)1/2(r2/(r2
- x2))1/2dx
= 4π∫0rrdx = 4πr2.
良く知られているように dV/dr = S である。このことを解釈すると, 基本的に球の体積は図のように球 (sphere) の薄皮に微細な厚み dr を掛けてそれを 0 から r 迄積分したものに等しいということになる。これが高次元の場合に役に立つ。

実際, n 次元球 (Dn : x12 + x22
+ … + xn2 ≦ r2) の体積は
V = (rπ1/2)n/Γ(n/2 + 1)
である。Γ
函数については円周率のところで述べたとも思うが,
細かいことはともかくとして, 結果だけ書くと:
V = rnπn/22n/2 / (2・4・6…n), n が偶数のとき,
V = rnπ(n-1)/22(n+1)/2 / (1・3・5…n), n が奇数のとき。
この積分は解析概論 第 8 章 練習問題(8) の (4) によれば, Dirichlet 積分から求められると書いてあるが, n 次元の極座標を使っても計算できる。
これから n - 1 次元超球面 (Sn-1 : x12 + x22 + … + xn2 = r2) の面積 (?) は r でこの式を微分すればいい事がわかるわけである。
参考文献:
高木貞治, 解析概論 改訂第三版, 岩波書店。
前へ
次へ
球の目次へ
Miscellaneous の index へ
HOME