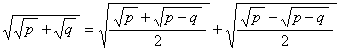.20世紀後半になって, 力学系の研究に最も大きな質的変化をもたらしたものは, computer の発達であろう。 高性能･高速化した computer は, Poincaré が "描こうとも思わない" と表現した chaotic な現象をいとも簡単に描いてみせ, chaotic な現象も多くの人達の共通認識となりつつある。 しかし, 20 世紀後半の力学系の研究が Poincaré が示した方法にどれだけの新しいものを付け加えることが出来たのだろうか, と感じているのは私だけだろうか。
彼は数学をやるのには十分な Fantasie がなかったから小説家になったのだ。
有名な de Moivre の公式は de Moivre (1667--1754, UK) の著作 「級数と求積に関する数学雑録」 (London, 1730) の一頁目に出ているという。
有名な二項定理の発見は Sir Isaac Newton (1642--1727) で, 1665 年頃のことであるという。 文献的には 1676 年 6 月 13 日付の手紙の中に初めて見られるという。 カジョリ 「初等数学史」 (共立出版, p. 340 参照)
発見を定義に取り込むと論理上の透明度は確かに増すが, 事の本質はその都度, 僕らの眼前から見失われてしまう。 微分係数は保持されても, 微分の意味はもう分らない。 論理の確保は言わば不可避の代償として, 僕らは歴史の喪失という大きな犠牲を払っているわけである。
自然対数の底 e
のことを双曲線対数と呼ぶことがあるのだそうだ。
これは直角 (等辺) 双曲線 xy = 1 と x 軸, 二直線 x = 1, x = t
で囲まれる部分の面積 S が S = ∫1xdt/t = log x
と表わされるところから来ていると言う。 この事実は 1647
年グレゴアール･サン･ヴァンサン (ベルギー, 1584--1667)
によって発見されたという。
カジョリ ｢初等数学史｣ (共立出版) p.235参照のこと。
三辺の長さが全て整数である三角形において, それら三辺の和とその面積とが等しくなるような三角形は, その三辺の長さが, (6, 8, 10), (5, 12, 13), (9, 10, 17), (7, 15, 20), (6, 25, 29) であるものに限る。 (これらは全て, 整数辺長の直角三角形 [ピュタゴラス三角形] からピュタゴラス三角形を 「引いた」 ものになっている) そして (整数辺長ではなくとも) 三辺の和と面積とが等しい三角形においては, その内接円の半径は2になる。
円のコーツの性質:
x2n + 1 = Πk=1n(x2 - 2x cos((2k - 1)π/(2n)) + 1).
初項 a 公比 r の等比数列の第 n 部分和の公式の証明:
Sn = a + ar + ar2 + …… + arn-1
= a + ar + ar2 + …… + arn-1 + arn - arn
= a + r(a + ar + ar2 + …… + arn-1) - arn
= a + rSn - arn
= rSn + a(1 - rn)
より (1 - r)Sn = a(1 - rn).
リサジュー図形はアメリカの科学者ナタニエル･ボウヂッチ (1773--1838) によって 1815 年に発見された。 (F. Cajori History of Physics, pp. 288-289)
アメリカでは, 日本で言う 「将棋倒し」 を 「望遠鏡的和」 と言うようである。
メルカトール図法は, 屡々誤って円柱投影図法であるかのように説明されるが, 実は, 球面 x2 + y2 + z2 = 1 から平面 w ∈ C への等角写像 w = i log((x + iy)/(1 - z)) である。 メルカトールがその地図を描き, 1599 年にイギリスの数学者エドワード･ライトが数学的説明を与えた。 その際に彼は ∫0θsec t dt を数値積分した。 1614 年にネイピアが対数表を発表, イギリスの数学者エドムンド･ギュンターが 1620 年に log tan θ の表を発表する。 1640 年に数学教師ヘンリ･ボンドはこの表とライトの説明中に現れる表とを比較して ∫0θsec t dt = log tan(θ/2 + π/4) を予想。証明は 1668 年ジェイムズ･グレゴリによってなされた。 我々が今日知っているような証明はアイザック･バロー (1630--1677) に拠る。 (Eli Maor (エリ･マオール) Trigonometric Delights 新しい三角法の世界, 好田順治訳, 青土社)
[結婚定理] #で集合の濃度を表すものとする。 B
を任意の集合とし, 各 b∈B に対し, G(b) を有限集合として,
∀B'⊆B (#(B') = k ⇒ #(∪b∈BG(b))≧k)
とする。 このとき, B 上の一対一写像 f で ∀b∈B (f(b)∈G(b))となるものが存在する。
これを結婚定理と呼ぶのは, B = boys の集合, G(b) = 「boy b
の知り合いの girls の集合」 と解釈すると分かる。 (渕野昌,
離散数学-集合の宇宙での数学入門 --- 第 11 講命題論理 23
結婚定理, 数学セミナー (10), 1999)
JPEG file は先ずもとの画像からの 8×8 の領域を sampling
した後, その 64 画素の color 情報を DCT (Discrete Cosine
Transformation 離散余弦変換) 処理をする。 その式:
Suv = (1/4)CuCvΣx=07Σy=07(Pxy
- Ls)cos((2x + 1)uπ/16)cos((2y + 1)vπ/16).
ここで, (x, y) は block 内の画像の位置で, (u, v) は DCT の出力 index, Pxy は座標 (x, y) の点の 「色」。 又, C0 = 1/√2, C* = 1 (*≠0); Ls は Pxy が 8 bit の精度のとき 128, 12 bit 精度のとき 2048 とする。 (森山弘樹, 特集ファイルフォーマット辞典, C magazine (10), 1999)
公式:
.
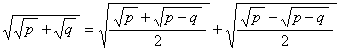[レーマスの不等式, 1820] a > 0, b > 0, c > 0 のとき abc
≧ (b + c - a)(c + a - b)(a + b - c) 或いは a(a - b)(a - c) + b(b -
c)(b - a) + c(c - a)(c - b) ≧ 0, いずれも等号は a = b = c に限る。
[Schur (?) による拡張] 更に μ≧0 のとき
aμ(a - b)(a - c) + bμ(b - c)(b - a) + cμ(c -
a)(c - b) ≧ 0, 等号は a = b = c に限る。
[数学セミナー (7), 1988]
対数螺線 (等角螺線) r = keaθ, k > 0, a > 0
に関し, 原点から x 軸上の点 T(ke2anπ , 0) 迄の長さは,
T でこの螺線に引いた接線が x, y
両軸で切り取られる長さに等しく
である。 [Evangelista Toricelli, 1608-1647]
Möbius band の parameter 表示:
x = (a - r sin(θ/2))cosθ,
y = (a - r sin(θ/2))sinθ,
z = rcos(θ/2).
但し , 0 < b < aでa, bは定数。
Homological algebra (ホモロジー代数) はフランスの解析学者 Jean Leray が故あって研究した fiber 空間の homologie の構造を調べるうちに見出した idea である。 Leray が反ナチスの抵抗運動の故捕らえられた収容所の中で作り上げ, 1945 年の解放後直ちに公表された理論で, 解析学での逐次近似の手法を代数化した system である (陳省身の評)。[堀田良之, 数学セミナー (2), 2000]
△ABC の内心を I, 内接円, 外接円の半径を各々 r, R
とするとき
AI・BI・CI = 4Rr2.
[東京都, 渡辺中, 15歳 (当時), 数学セミナー (3), 2000]。
定理 [D. J. Velleman, 1997]
写像 f : En → En (En は n 次元 Euclid
空間) が連続であるためには,
任意の連結集合の像が連結で任意の compact 集合の像が compact
であることが必要充分である。 [Characterizing Continuity, Amer.
Math. Monthly, 104 (1997), 318-322]
定理 [浦崎幸士, 1999]
同様のことが局所連結な距離空間 X から距離空間 Y
への写像 f :X → Y に関しても成立するが,
連結なだけの距離空間 X 上の実数値函数 f : X → E1
に対しては成立しない。 [連続写像の研究,
静岡大学大学院教育学研究科修士論文]
Beta函数はJacques Philippe Marie Binet (1786-1856) の論文「Euler の定積分について」(理工科学校雑誌16,
pp. 123-343) に於いて導入された。この函数は第一種Euler積分と呼ばれることもある。
Gamma函数の考察はEulerに始まる。Gamma函数という呼称と表記記号
Γ(x) はAdrien Marie Legendre (1752-1833)
に由来する。初出は「様々な位数の超越函数と面積の算出に関する積分計算演習」(全三巻)
の第二巻 (1914)。Legendre自身は第二種Euler積分と呼んでいたが,
彼以降gamma函数という呼称が定着した。
拡散過程を多様体と思う時, その接空間に当たるものがブラウン運動である。
五角数定理 [L. Euler, 1741]
これの証明の概略は
と置くときに,
を示すのだそうだ。
Omnia seu finita seu infinita definita sunt et excepto Deo ab intellectu determinari possunt. (有限であれ無限であれ確定したるものはすべて, 神は別として, 知性により決定されうる。)
有名な Pascal の三角形に関して, Pascal が示した original の式は nCk : nCk+1 = (k + 1) : (n - k) で証明は数学的帰納法であるという。 これは死後出版された 「数三角形論」 に出ているという。 (算術三角形論は 1654 だが, 元の数学者朱世傑の四元玉鑑, 1303 にも同様の記述あり。又 1527 年の Petrus Apianus の 「算術」 という本にも出ている)
「数学的帰納法」という名前は 1838 年の 「ペニー百科事典」 の中で de Morgan が書いた記事中にあるのが初出であるらしい。
√2 は完全に明らかな何かと見なすのに, √(-1) の前では尻込みをする多くの人が確かにいます。 前者は物理空間の中の何とか眼で見ることが出来るのに, 後者はそうでないと, その人たちは考えるのです。実際には, √(-1) の方がずっと単純な概念なのですが。
複素数の平面ベクトルとしての表示は, 1797 年にデンマーク科学アカデミーの集会で Casper Wessel (8th June 1745--25th March 1818) が報告したのが最初で, 彼が本に書いたのが 「方程式の解析的表現について」 (1799) だった所為か, 1806 年に自費出版で発表した Jean Robert Argand (18th July 1768--13th August 1822) の名前を冠して Argand diagram と呼ばれている。
人類が数に関わる問題を考え始めた頃は,
重要な問題の多くに次々と望ましい答えが出てきたのに, 19,
20 世紀になってくると, 数学者たちは, 殆どの重要な問題は,
我々が望むような形では解くことが出来ない,
ということに気づいたのである。
丁度, 科学文明の始まりでは,
自然は科学の進歩によって人間の望む通りに,
好きなように変えられるし,
重要なことで科学に解明できないことはない,
と信じていたのが,
誤りであることが明らかになってきたように。
0 < a1 ≦ a2 ≦ … ≦ an , pi
> 0, のとき,
,
と置けば A ≧ G が成り立ち, 等号成立は a1 = a2 = … =
an のときに限る。 [Alzer Horst, A Proof of the Arithmetic Mean-Geometric
Mean Inequality, American Mathematical Monthly, vol. 103, no. 7, p. 585, 1996.]
証明:
まず, n = 2 の場合を考える。 このとき, a1 ≦ G ≦ a2
は明らかだから, a1 = a2
でない限りそこの等号も成立しないので 
が成立する。 ここでの等号も a1 = a2
のときのみであることも明らか。 従って
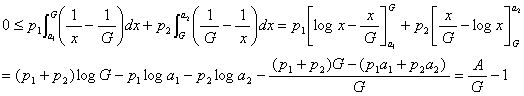
なので, この場合には A ≧ G が成り立つ。
等号成立も同様である。
さて一般の場合, ak ≦ G ≦ ak+1 となる k が存在する。この
k を用いて
等号成立に関してもすぐに分かる。
周期 1 の函数 f に関し, Fibbonacci 数列 Fn を用いて
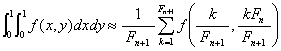
という近似公式が成立する。[Hua Loo-Keng (華羅庚) & Wang
Yuan, Applications of Number Theory to Numerical Analysis, Springer, 1981]
33 + 43 + 53 = 63,
44 + 64 + 84 + 94 + 144 =
154,
304 + 1204 + 2724 + 3154 = 3534,
45 + 55 + 65 + 75 + 95 +
115 = 125,
275 + 845 + 1105 + 1335 = 1445,
958004 + 2175195 + 4145605 = 4224815,
26824404 + 153656394 + 187967604 = 206156734,
182 + 192 + … + 282 = 772,
382 + 392 + … + 482 = 1432,
72 + 82 + … + 1902 = 15182,
202 + 212 + … + 3082 = 31282,
10812 + 10822 + … + 15382 = 281672.
= という記号を作った人は Robert Recorede, 1510--1558 The Whetstone
of Witte (1557)
+ , − は Johannes Widmann (ドイツ), 1462--1498.
÷ は Johann Heinrich Rahn (スイス) 1622.3.10--1676. (実は 1000年昔からあったものを再利用した。
日米英以外では余り使われていないらしい)
× は William Oughtred (イギリス), 1574.3.5--1660.6.30 Clavis Mathematicae
√ は Christoff Rudolff, 1499--1545.
<, > は Thomas Harriot (イギリス) 1560--1621.7.2.
この項目に関して Geometry.Net --- Scientists: Rudolff Christoff という所に link されている (no. 84)。
円周率の近似値 (by ラマヌジャン)
黄金分割比の連分数表示。
右辺の方の 2 の冪指数にFibonacci列が出ていることに注目。
正 257 角形を定規とコンパスのみで作図する方法は 1832 年にリヒェートが考えたという。
自然数の逆数の無限和が ∞ になることを証明したのはオーレムという人で, 1350 年頃のことであるという。
相異なる素数 p, q に対し pq という形の完全数は 6 だけである。又 p2q という形をした完全数は 227 = 28 だけである。更に n が 2 以上の自然数で 2n−1 が素数であるとき, 2n−1 (2n−1) は完全数で (ユークリッド 「原論」 IX 36), 逆に偶数の完全数はこの形のものに限る (Euler)。
メルセンヌ素数に関する最新情報の page: http://www.mersenne.org/
一次元及び二次元の酔歩に関する理論では次の三つのことが知られている:
i) 原点から出発するとき, 確率 1 で,「有限時間 R で原点に戻る」。
ii) 時間と共に i) は繰り返し起こるので, 確率 1 で,
酔歩は原点に無限回戻る。
iii) 一方, 原点から原点に戻るまでの時間間隔の期待値は,
それぞれ ∞ である。
これらは大偏差原理と呼ばれるものの一種である。 この,
特に iii) から, 勝つときは勝ち続け,
負けるときは負け続ける, という 「勝負運」
があることが数学的に立証されていると思って良い。
生態系の植物相を決めるのは大偏差原理である。外来種が闖入して来て何年かはびこることは良く起こるが, 10 年 20 年に一度は必ず来襲する大寒波により殆ど総て淘汰されてしまう。
幾つかお金が入っている袋がある。その中に偽金だけが入っている袋が又幾つかある。本物のお金が入っている袋は本物だけが入っているとし, 本物のお金は総て 1 g, 偽金は総て 1.1 g としよう。はかりを一度だけ用いてどの袋が偽金かを調べるにはどうしたらよいか。 但し, 一袋には必要なだけ十分な枚数が入っているとし, はかりは必要なだけ十分重い重さが計れるものとせよ。
解答:
袋に番号をつけ, 0, 1, 2, 3, 4, 5, …, n としよう。各袋から k
番目からは 2k 個だけ取り出す。総計 n(n+1)/2 個だから,
総て本物とすれば n(n+1)/2 g であるが,
実際にはそれより重いはずである。その差を x / 10 g
とすれば x を 2 進表示したときの, bit の立っている桁 (0
でない桁) が偽金が入っている袋の番号を示している (下から
0, 1, 2, … と数えなければならないが)。
数学と小論文は異常なまでに出来た。 他は全滅。 国語なんて, 他人が書いたものを理解するのは無理だよ。 その点, 数学は何も覚えなくてもいいし, 全部その場で定理を証明すればいい。 模擬試験で全国一位も取った。 でも, 覚えることは今でも本当に駄目。 歌詞も覚えられません。
電車の長いシートで一人分ずつの区切りを無視して, 無作為に席を取ると無駄な隙間がいっぱいできる。 この時, シートが無限に長いなら, 座席定員の約四分の一は無駄になる。
Microsoft Excel 2000 で = -1 ^ 2 って入力すると幾つが表示されると思います ? なんと 1 になっちゃうんですよ。困りましたねぇ。
√2 = a/b と既約有理分数表現出来たとすると, 明らかに b > 1. そこでこの両辺を自乗すると 2 = a2/b2 で, 両辺とも既約有理分数であるから b2 = 1 でなければならないがそれは矛盾である。
二次方程式を実数体上代数的に解くことは 12 世紀のインド人, バスカラによってほぼ完全に解かれた。三次方程式のうち x3 + ax = b の代数的解法はフェッロによるらしい。
常微分方程式
に関し, 解は無数に存在し
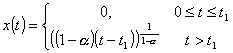である。 [ペアノ-オスグッドの性質]
この本の中に方程式を一つ入れるたびに, 売れ行きは半減すると教えてくれた人がいる。 そこで方程式はいっさい入れないことに決心した。 しかし, とうとう一つの方程式だけは入れることになってしまった。 アインシュタインの有名な方程式 E = mc2 である。これが私の本の潜在的読者を怯えさせ, 半分に減らさないことを願う。
人々は神や方程式 (時には同時にその両方) に頼ったり, 戯曲を書いたり, 蟻の研究に打ち込んだりしてその [自然の本質, 真理の本質とは何かという] 答えを探す。 ところが面白いことに, 光線が波打つ電磁場であることの発見に役立ったのと同じ考え方が, 様々な社会問題の原因究明にも役立つのである。 (中略) 方程式は経済情勢, 疾病の pattern, 人口増加から偏見や差別の影響まで探り出し, これを量で表す。 数学は文字通り私達の意識を拡張し, もっとたくさんのものを見せてくれる。
数学は単純であるから普遍性がある。 日常生活でも似たようなことが言える。 包丁一つあれば, 菜っ葉も刻めるし, 大根の皮もむける。 しかし (中略) 単純ということは易しいということではない。