1999 年の column

数の集合を表す時には, 例えば自然数の集合を N, 整数環を Z, 有理数体を Q, 実数体を R などと表すように, 最近では白抜きの太字で表すことが多い (すいません HTML だと出せないもので...)。今は亡き前原昭二先生は, これは日本人が始めたので Japanese bold font というのだと言っていた。あちらの人はどうしているかというと, 只単に大文字で黒板に書くのだという。AmSTeXではこの字体のことを blackboard bold と呼んでいる。
　(編集者への注: AMSTEX がこの形 (M と E が下がった形) で印字できないときは, 国際的にAmSTeXと印字することに決まっている) (と書いたら, この注もそのまんま本に載せられてしまった !!)

空集合を表す記号は屡々誤ってギリシャ文字の φ が用いられるが, 本当は「0に斜線」 である (Donald E. Knuth による)。この記号は André Weil がノルウェーの文字 ø から採用したという (ドイツ語の ö や フランス語の œ と同じような発音をする)。きっと, ノルウェー語では空 empty という単語が ø から始まっているのだろう。 (と書いたら, 今度は ø がギリシャ文字で印字されてしまった !!)

無限大を表す記号 ∞ は Wallis が考えたのだそうだ。

秋山仁による二次行列での Cayley-Hamilton の公式の証明。

公式 [横田, 大阪府清風南海高校]

_n+rC_r+1 = Σ_{k = 0}^n-1 _r+kC_r.

[証明] (この証明は星野敏司, Sunday 27^th September 1998.)

n = 1 の時 _n+rC_r+1 = _rC_r は自明。

n = N + 1 の時

_{(N+1) + r}C_r+1 = _N+rC_r+1 + _N+rC_r = Σ_{k = 0}^N-1 _r+kC_r + _N+rC_r = Σ_{k = 0}^(N+1)-1 _r+kC_r .

同様にして _nH_r+1 = Σ_{k = 1}ⁿ _kH_r も分かる。これらの何れかを用いて数学的帰納法で, 次が証明できる [井上･横田]:

.

科学の世界は大体数学的かというと, 意外にそうでもない。数学の世界では自乗と掛算とどっちが先かと訊かれれば, 迷うことなく自乗であると答えるだろう。例えば ax² は a(x²) であって, (ax)² ではない。ところが km² 等というのは, 1, 000, 000 m² であるので, 掛算の方が優先されている。自乗を優先して考えれば 1000 m²であるはずだ。日本人は km² を「キロ平米」などと読むが, これはどう考えてもおかしいと思うが, どうだろうか。

普通, 全く同じ数量に対し, 同じ単位が付いているということはないが, 通常使われる単位では例外が 2 つあるように見える。本当の例外は kl と m³ である。もう一つ例外に見えるのは ml と cm³ と cc だが, よく考えてみると, ml と cm³ は kl と m³ から単位換算しただけだし, cm³ と cc に至っては全く同じものである。抑々 cc というのは辞書を引いてみると分かるが, cubic centimeter 即ち cm³ の英語読みの省略形に過ぎない。

国際単位の中で日本人 (のみならず東洋人) の名前が使われているのは唯一 Y (ユカワ) という長さの単位だが, これが不幸にして fm (フェムトメートル) という長さの単位と等しいため, 欧米人たちは Y を使わず fm を好んで使いしかもフェルミと読んでいる。(因みに1 Y = 1 fm = 10^-15 m)

詩の形で書いてある computer program の例:
This algorithm to count bits
Rotates VALUE one left and sums its
　　　　two's-comp negation
　　　　in a zeroed location
Repeats WORD LENGTH times, then exits.
これは正しく実行できる。この algorithm は sideway addition 手法と呼ばれる高速なものである。(これぞ文芸的 programming !) (出典は Mathematical Writing by Donald E. Knuth, Tracy Larrabee, and Paul M. Roberts, 有澤誠訳, 共立出版「クヌース先生のドキュメント纂法」第 43 章 最後のまとめ 第 31 回講義記録 後記 p.185.)

Pythagoras 数の中で, 直角を挟む二辺の数が連続しているものの例: (20, 21, 29), (119, 120, 169), (803760, 803761, 1136689). [大矢真一, ピタゴラスの定理, 東海書房, 1952, pp.48--49.]

André Weil, 1906--1998 の言葉:
　　勿論数学も芸術の一部だ。
　　数学は人間の精神の栄光のためにあるのだ。

大学初年度の線型代数の問題:
1. 行列 A は冪零 nilpotent (say Aⁿ = 0) とする。この時, A - I (I は単位行列) は正則である (i.e. 逆行列を持つ) ことを証明せよ。
2. 行列 B は 3 次以上の正方行列とする。この行列が関係式 B³ + 2B + I = 0 を満たしているとき, 行列 B - I が正則であることを証明せよ。

解答
1. (A - I)^-1 = -Σ_{k = 0}^n-1A^k だから (等比数列の和の問題)。
2. (B - I)^-1 = -(B³ + B + 3I)/4 だから (整式の割り算の問題)。

筆者が微分積分の最初の所を教えるときにふと頭に浮かぶ白居易の一節

在天願作比翼鳥 在地願為連理枝

(読み方と意味は国語の先生にでも聞いてください。長恨歌 ll.117-118)

素数列 {p_n} = {2, 3, 5, 7, 11, 13, 19, 23, …} の絶対的階差数列 {p_{1, n}} = {|p_n+1-p_n|} を考え, その又絶対的階差数列 {p_{2, n}} を考え ... とやっていくと p_{m, 1} = 1, m ≦ 63418 が知られているそうである。(一般ではopen question) (David Wells Hidden Connections, Double Meanings---A mathematical exploration, 大橋義房訳「みつけよう! 数学!」, 岩波書店, 第 17 章 類型認識と錯覚, 問題 6, 解答 p. 251)

sin x の (2n + 1) 倍角の公式:

勿論 n は非負整数。証明は頑張れば帰納法や, Euler の公式を使えば出来る。

実はこの公式は次のように拡張できる。μ∈R, |x| < π/2 の時,

証明は難しくない。ただし、計算が大変である。概略をいうと, |x| ≦ 1 の時,

という級数展開式を証明し, x のところに sin x を代入すればいいだけである。
(一松信他, 『数学公式 II』, 岩波書店, 1986)

前々から, 天文学と数学には深い関係があると思っていたが, ついにインテグラル星雲というのがあることを見つけた。 http://heritage.stsci.edu/public/forms/gal_desc.html#3697 を見ていただくと (まだあるかどうか不明なので link していない),
UGC 3697, commonly known as the "Integral Sign Galaxy", displays a "sum" of many intriguing phenomena. Located in the constellation Cameleopardis ("the Giraffe"), UGC 3697 was likely once a flat, rather unspectacular disk galaxy.
という記述があった。

[倍数判定法]
整数が2, 3, 4, 5, … 等で割り切れる条件を知っている人は多いだろう。実は更に次の性質が成り立つ。
先ずxを非負整数とし, その十進表現を x = Σ_{n = 1}^∞10^n-1x_n, x_n ∈ Z, (x_n = 0 for a.a. n ) とする。

x ≡x₁ (mod 2),
x ≡ Σ_n=1^∞x_n (mod 3),
x ≡ 10x₂ + x₁ (≡ 2x₂ + x₁) (mod 4),
x ≡ x₁ (mod 5),
x ≡ x₁ -2Σ_n=2^∞x_n (mod 6),
x ≡ Σ_n=1^∞(-2x_6n - 3x_6n-1 - x_6n-2 + 2x_6n-3 + 3x_6n-4 + x_6n-5) (mod 7),
x ≡ 100x₃ + 10x₂ + x₁ (≡ 4x₃ + 2x₂ + x₁) (mod 8),
x ≡ Σ_n=1^∞x_n (mod 9),
x ≡x₁ (mod 10),
x ≡ Σ_n=1^∞(-x_2n + x_2n-1) (mod 11),
x ≡ x₁ - 2x₂ + 4Σ_n=3^∞x_n (mod 12),
x ≡ Σ_n=1^∞(4x_6n + 3x_6n-1 - x_6n-2 - 4x_6n-3 - 3x_6n-4 + x_6n-5) (mod 13),
&c.
無限和になっているところは, 勿論再帰的に利用できる。証明は ... 思いつきますよね。
(参考文献: Cornelius Lanczos: Numbers Without End. 米田桂三訳「数とは何か」講談社 Blue Backs #269.)

上記の mod 7 の部分が誤って x ≡ Σ_n=1^∞(2x_3n -3x_3n-1 + x_3n-2) (mod 7) になっていたので, 訂正した。 又 「数学質問箱」 の掲示板で 「我疑う故に存在する我」 氏から指摘のあった, mod 8 の部分, 及びそれからすぐに思いつく mod 4 の部分の括弧内を加筆した。 [Wed, 11th Feb, 2004]

正則連分数

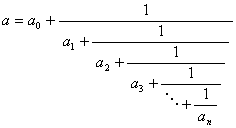
を早く計算するには, 行列を使って

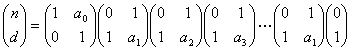
とするとき, a = n/d とすればよい。(問題: 正則でない (即ち分子が 1 とは限らない連分数は ?)

素数の集合を P, 集合の濃度を Card で表すとき, 記号 π(x) = Card{y | y∈P, y ≦ x} は N. Nielsen: Theorie des Integrallogarithmus (1906) による。

函数 f(x), g(x) が x →∞の時に漸近収束する (i.e. f(x)/g(x) → 1) 時, f(x) 〜 g(x) と書くが, これはP. du Bois Reimondによる。

形や形態というと, 多くの人は, 固定的に静的に捉えがちである。だが, 静的に見ている限り, 形態の本質は何も明らかにされない。(中略)
　幾何学的定理の証明に使われる, 所謂補助線というのは, 動的な思考を行えば自然に "見えてくる" ものであり, 実際には "補助" ではなく, 考察下にある対象の幾何学的関連の一部をなすものなのである。只, 静的な思考にとどまる限り, その関連が見えないだけに過ぎない。動的な思考を通して, この関連が見えた瞬間, 考察下にある定理は自明のものとなる。幾何学に限らず, 真の数学的思考というのは動的なものであって, この生き生きとした動的思考によって, 悟性的･静的な思考では見ることの出来ない, 或いは閉ざされたままにとどまる, 対象の本質が明らかにされるのである。この時, 私達は, 世界のより深い相に突入し, 感覚的･悟性的思考には隠されている神的な秩序或いは真理を垣間見ることになる。
[脚注に移って] 余談であるが, 筆者は, 数学を学ぶことの最大の人間的意義或いは価値は, ここで述べた意味での動的思考を学ぶこと --- それは決して易しいことではないが --- にあると考えるものである。 数学の経験において獲得される動的思考の精神は数学の領域を超えて他の諸領域 (感覚的･物質的領域だけでなく心魂的･精神的領域も含む) へと拡大することが可能であり, 世界の根底に横たわる神的秩序と真理 --- それは, 感覚的･悟性的思考には隠されている ---, を数学におけるのと同種の明晰さと厳密さを持って認識することを可能にするのである。
　この意味で, 数学の精神はあらゆる学問の基礎たり得るだけでなく, 既成の学問領域を超える無限の可能性を秘めていると同時に, 私達を真の霊的な高みへと導く手段の一つを提供するのである。 あの偉大なピュタゴラスやプラトンが数学を宗教或いは哲学の基礎として重要視したのは, まさに, 数学の精神性が有するこの, 人間の魂を浄化し, 魂に光を与える比類ない力の所以なのである。

恒等式 (5 + x)(5 + y) = (5 - x)(5 - y) + 10(x + y) は誰でもすぐに証明できるが, これを掛算九九で 5 を超えるものどうしの掛算をするときに利用するということを考えた人がいる。
例えば 7×8 を計算するときに, 左手で 7 を数えると, 2 余るので 2 本指を折っておき, 右手で 8 を数えると, 3 余るので 3 本指を折っておく。つまり 2 が x, 3 が y ということになる。当然 (5−x) が左手に立っている指の数, (5−y) が右手で立っている指の数である。だから, 左右の立っている指の数を掛けてその数の 10 の位に, 左右で指を折った数を足した数を足す。そうすると掛算が出来たことになる。(ニッポン放送: 日曜夕方トコロのココロエ, 7th Feb, 1999による)

Concert hall に言ってみれば分かるが, そこには不釣り合いなほど多くの数学者がいる。 数学の創造と音楽への関心には深い関係があるのかもしれないが, 解明することはかなり難しい

A. N. Kolmogorov, 1903--1987.

今の算術に用の用あり, 無用の用あり, 無用の無用あり。

Fable が昆虫を追いかけたのも, Mendel がエンドウを栽培したのも, それは彼等にとって仕事ではなく, 自由な時間に没頭する楽しみ事であった。Darwin が南米や南太平洋諸島で, 動植物を観察したのも, またしかりである。そこにはいずれも, 職業と化した学問研究とは何処か異なる, 精神の豊かさが感じられる。さればこそ, 学問はやはり道楽として楽しみたいものである。

予想 [E. Catalan, 1844]
m, n, p, q が1より大きな整数の時, m^p - n^q = 1 は 3² - 2³ = 1 以外の解を持たない。
定理 [R. Tijedeman, 1976]
定数 C が存在して, m^p - n^q = 1 (p, q > 1) が成立すれば, m, n, p, q は何れも C より小さい。
実質的に分かっているのは C ≦ 1.06×10²⁶.
予想 [S. S. Pilai, 1936]
k ≧ 2, p ≧ 2, q ≧ 2 とすると, m^p - n^q = k を満たす数の組 (m, n, p, q) は有限個しかない。

論理学は Aristotle に始まる。それは哲学の議論を検討する道具(オルガノン)として作られた。現代の論理学は寧ろ数学に近いが, 最初は言葉や文について研究する学問だったのだ。だから今でも大学では, 哲学の一部分として文学部の中に論理学がある。
近代に至るまで, 論理学は「三段論法」を中心として, 命題の真･偽 (論理値) を判定するというものだった。だが, 19世紀, イギリスの数学者 Boole は,「真･偽も, 代数的な方法で取り扱うことが出来る」ということを示した。記号論理学の誕生である。現在, 真･偽だけを取る値を「ブール値」, ブール値を扱う代数を「ブール代数」というが, それは彼の名前に由来している。
今日, 多くの programming 言語で真･偽を代数的に扱える。それも Boole のおかげなのである。

三辺の長さが整数で表される直角三角形はその面積も全てが整数であるが, 三辺の長さの合計が面積と等しくなるものは (8, 6, 10) と (5, 12, 13) だけである。これは, Brahmagupta の定理 (岩波数学辞典第 3 版 355 不定方程式 A) から簡単に証明できる。
整数と限らなければ, 三辺 (k(1 - t²)/(1 + t²), kt²/(1 + t²), k) と表すとき, k > 4 + 4×2^1/2 である限りに於いて t = (k ± (k2 - 8k -16)^1/2)/2(k+2) であるものがそれである (± はの違いは直角を挟む二辺を交代させるだけである)。尚この時, 三辺の長さの和と面積は共に 2(2 + k) になるので, k が整数 n でもって n/2 と表されるときには必ず三辺の長さの和も面積も整数になる。

前へ
次へ
コラムの墓場の目次へ
HOME