2004 年の column
正整数 a, b (a > b ≧ 1) が互いに素ならば, ax + by = 1 を満たす整数 x, y が存在する
[証明] a + b = n ≧ 3 に関する数学的帰納法で証明します。
n = 3 のときは, a = 2, b = 1 なので, (x, y) = (1, -1) なので成り立ちます。
n = k 以下のとき成り立つと仮定します。 今, c = a - b とおくと, b と c は互いに素であり b + c = b + (a - b) = a
< a + b = k + 1 なので, 帰納法の仮定から, bu + cv = 1 となる整数 (u, v) が存在します。 ところが, bu + cv =
bu + (a-b) v = b(u - v) + av = 1 なので, (x, y) = (v, u-v)とすれば, ax + by = 1 となり, k
+ 1 の場合も成立します。 Q.E.D.
野崎昭弘、仙波一郎共著
計算の理論
放送大学教育振興会 1995
要するにこれはそういう x, y を求める (再帰的) algorithm であるわけだ。
Sunday, 5th September, 2004.
32 + 42 = 52,
102 + 112 + 122 = 132 + 142,
212 + 222 + 232 + 242 = 252
+ 262 + 272,
362 + 372 + 382 + 392 + 402
= 412 + 422 + 432 + 442,
552 + 562 + 572 + 582 + 592
+ 602 = 612 + 622 + 632 + 642
+ 652.
各点収束のみで函数列の極限を扱うことの不備を指摘したのは Abel (1826), 一様収束を考えたのは Weierstrass.
内積は Grassmann によって導入され, [a | b] と書かれていた。 Hamilton
が四元数を考えたとき, a + bi + cj + dk の bi + cj + dk の部分をベクトル部と呼んでいた。
このベクトル部同士の積のベクトル部を外積と呼んだ。 四元数として, 純ベクトル四元数 (実部が 0 の四元数) α, β の積は αβ = -α・β + α×βとなる
(・は内積)。
欧州の数学史上で最も早くこの思想 (行列式) の現れたのは Leibniz が 1693 に l’Hospital へ送った書簡中であるが, これは
1850 にゲルハルトが Leibniz の遺稿中から発見するまでは全く埋もれていた。 従って行列式の理論の発展には直接の影響を与えなかった。
行列式の理論の実際上の源泉は Cramer が 1750 に公にした代数曲線に関する書であって, Leibniz と同様に,
やはり一次方程式の一組の解から出発している。
藤原松三郎
代数学, 第一巻
一階非線型連立常微分方程式
x' = y – x3 + x
y' = -x
を Van del Pol 方程式と呼ぶが, これを一般化した
x' = y - f(x)
y' = -x
は Lienard 方程式と呼ばれている。
座標を使うこと自体は目新しいことではない。プトレマイオスは既に二世紀の段階で, 地図の中で座標を使っていた。 デカルトのアイディアの真に先進的なところは,
座標そのものではなく, それをどう使ったかなのだ。
レナード・ムロディナウ
(青木薫訳)
ユークリッドの窓 平行線から超空間に至る幾何学の物語
Wednesday, 14th April, 2004.
四重友愛数の桁数の世界記録は日本人が持っている。
正矢 (1 - cos θ), 余矢 (1 - sin θ) は 「測量全義」 第七巻 「球面曲線形」 に出ているらしい。
各面が合同な三角形になるような四面体を等面四面体と呼ぶ。
(1) 等面四面体の面は鋭角三角形であり, 任意に与えられた鋭角三角形を面とするような等面四面体は一意的に存在する。
与えられた直方体に対し, 一つおきに頂点を選び, その頂点とそれに最も近い三頂点とからなる四面体を四つ切り落とすとそこに四面体が残る。
これを直方体の内接四面体と呼ぶ。
(2) 直方体の内接四面体は等面四面体であって, その体積は直方体の 1/3.
(3) 任意の等面四面体はある直方体の内接四面体となり, その直方体はその等面四面体に対して一意的に定まる。
(4-a) 等面四面体の対辺の長さは等しい (直方体の対面の対角線)。
(4-b) 対辺中線 (対辺の中点を結ぶ中線) は対辺に直交する (直方体の対面に直交している)。
(4-c) 三本の対辺中線は一点で互いに直交する (その交点は直方体の中心である)。
(5) 等積四面体 (各面の面積が等しい四面体) は等面四面体である。[幾何学大辞典第二巻]
(6) 等面四面体では重心と外心と内心が一致する。
(7) 三辺が a, b, c の鋭角三角形を面とする等面四面体の体積は (1/12)√(2(u2 - v2 + w2)(u2
+ v2 - w2)( -u2 + v2 + w2)).
村崎武明
等面四面体から等面六面体へ
数学セミナー (3), 2004.
∫xkdx = xk+1/(k + 1) + Cは k = -1 の所だけ例外だが, C の所を -1/(k
+ 1) + C と書き直すと
xk+1/(k + 1) - 1/(k + 1) = (xk+1 - 1)/(k + 1) → log x (as
k → -1)
が言えて, k = -1でも連続であると考えられる。
配列数式:
Microsoft Excel を用いて, 例えばクラス毎の平均を出すときに, これを使うことが出来る。 クラスの番号 (別に桃組とかでも大丈夫だが) が
A2:A100 に入っており, 対応する得点が D2:D100 に入っているとしよう。このとき
=AVERAGE(IF(A2:A100=2,D2:D100))
と cell に入れて Ctrl+Shift+Enter を打つと 2 組の平均が出る (桃組なら ="桃" とする)。A2:A100 の所と D2:D100
の所の型 (行の数と列の数) は一致していなければならない。 この方式を使うと, 例えば得点順に sort
してクラスがバラバラになっても平均はクラス毎に出るので便利である (但し空欄が除外されないので, その生徒の所のクラス番号を消しておく必要がある)。(これは
「配列数式とその入力方式について」 という help の項目で見ることが出来る)
Saturday, 20th March, 2004.
二項係数は既に 11 世紀の中国で既に研究されていた。
根上生也
離散数学
数学セミナー (1), 2004.
自然数 n > 1 で Σk=0n k2 が平方数となるのは n = 24 のみ。
その時 Σk=024 k2 = 702.
宮本雅彦
有限群村の冒険
リーチ牧場
数学セミナー (1), 2004.
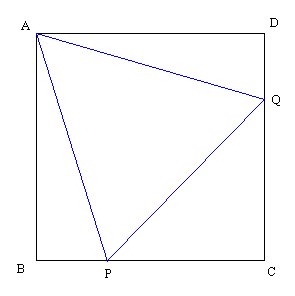 図で一辺 1 の正方形 ABCD に, 頂点 A
を共有して内接する正三角形 APQ が描かれている。 この時 ∠BAP = ∠DAQ = 15°である。 以下ではこれを用いて 15°,
75°の三角比を高校一年生程度の知識で求める。
図で一辺 1 の正方形 ABCD に, 頂点 A
を共有して内接する正三角形 APQ が描かれている。 この時 ∠BAP = ∠DAQ = 15°である。 以下ではこれを用いて 15°,
75°の三角比を高校一年生程度の知識で求める。
先ず AP = AQ = PQ の長さを求める。
これを x と置くと, △ABP で三平方の定理より, BP = √(x2 - 1), 従って CP = 1 - √(x2
- 1) (= CQ) である。 △CPQ が直角に等辺三角形であることから x = PQ = (√2)CP = (√2)(1 - √(x2
- 1)). これから x - √2 = -√(2(x2 - 1)). 辺々自乗して
x2 - 2(√2)x + 2 = 2(x2 - 1) = 2x2 - 2.
移項して整理すると
x2 + 2(√2)x - 4 = 0.
x2 + 2(√2)x + 2 = 6.
(x + √2)2 = 6.
x + √2 = ±√6.
x = ±√6 - √2.
x = AP であるから x > 0 なので, x = √6 - √2. 従って
cos 15°= AB/AP = 1/(√6 - √2) = (√6 + √2)/4.
又, BP = 1 - CP = 1 - PQ/√2 = 1 - (√6 - √2)/√2 = (√2 - √6 + √2)/√2 = (2√2 -
√6)/√2 = 2 - √3. よって
sin 15°= BP/AP = (2 - √3)/(√6 - √2) = (2 - √3)(√6 + √2)/4 = (2√6 + 2√2 - 3√2 -
√6)/4 = (√6 - √2)/4.
これらを用いて
sin 75°= sin(90°- 15°) = cos 15°= (√6 + √2)/4.
cos 75°= cos(90°- 15°) = sin 15°= (√6 - √2)/4.
一松信
数学 I・数学 A の活動実践事例
数学部会通信 No. 51, 2004.
神奈川県高等学校教科研究会数学部会
[Microsoft Word と field code]
Microsoft Word で数式を入力するのは, 付属の Equation Editor を使うのが普通であるだろうが, 実は, field code
というのを使うと簡単なものなら file を余り大きくせずに作ることが出来る。 先ず, field code というのは [挿入], [フィールド]
から挿入するか Ctrl + F9 で出て来る中括弧 { } の中に code を書き込んでいく。 例を見れば分かるように code
は大文字でも小文字でも問題なく作用する。 各々の switch については help で 「EQ \b」 とか入力すると細かいことが分かると思われる。
以下幾つか例を挙げる。
- 三行二列の行列: {eq \B \bc\( (\a \ac \co2 \vs2
\hs3(\f(3,5),12,21,22,31,32))} この中に出て来る \f(3, 5) は 3/5 を表示する。
- Σk=1n k = (1/2)n(n + 1). {EQ \I \su (k = 1,n, k)} =
{EQ \F(1, 2 )}n{EQ \b \bc\( (n + 1)}.
但し { } の外にあるのは普通の (field code ではない) 文字である。 又, 文字の大きさの関係を普通のものにする為には, 上下に付ける k
= 1 と n は (標準が 10.5 pt の場合) 9 pt 程度にする必要がある。 又 k や n は italic にするべきである。
- Πk=1n (1/k) = 1/n!. {EQ \I\pr(k = 1,n, \f(1, k ))} =
{EQ \F(1, n! )}.
- ∫0π/2 sin x dx = [-cos x]0π/2
= -cos(π/2) + cos 0 = 0 + 1 = 1.
{EQ \I\in(0,\s\up16 (\f( π ,2)), sin x dx)} = {EQ \b\bc\[ (−cos x)}{EQ
\o(\S\up16(\f( π ,2)),\s\do8(0))} = -cos {EQ \F( π ,2)} + cos 0 = 0 + 1 = 1.
ここで \f( π , 2) は 8 pt になっている。
- ∫1e dx/x. {EQ \I\in(1,e,\f( dx ,x))}
- 連分数 {EQ \F(1,1 + \f(1,1 + \f(1,1 + …)))} このあとに = を付けるとちゃんと最初の線の位置に来るので,
Equation Editor より便利である。
- 根号 3√(2/3) {EQ \R(3,\f(2, 3 ) )}
- 横断正則 (transversal) の記号 f {EQ \O(∩,|)} g. 但し | は 16 pt になっている。
- 空集合の記号 (0 に /): {EQ \O(0,\s\do2(/))}. 但し / は 18 pt.
- 写像の記号: f: a {EQ \O\al(\s\up3(|), →)} b. ここで | は 5 pt, → の前には 2 pt の space
が入っている。
- 四角く囲む {EQ \X(\f(3, 4 ))}
- 括弧の入れ子の例: {eq \b\bc\[ (sin \f(\b\bc\((n + \f(1, 3
))θ,8))\o(\s\up30(π),\s\do12(0))}
- field code 以外の要素を書いても問題なく動作する。 相加平均と相乗平均の例: {eq \f( a + b ,2) ≧ \r(,ab )}
例に見られるように入れ子にして使うことが出来る。 実際に打ち込んでみられることをお勧めする。 実際に入力する際は外側から入力しないと error
が出てどうしようも無くなってしまう。 (12 と 13 を Friday, 5th March,
2004 に加筆, Saturday, 20th March, 2004 にも一寸加筆)
Wednesday, 25th February, 2004.
Ash Wednesday.
二次元 Riemann 多様体 M の, 点 x から半径 r (> 0) 以内の点全体の成す領域の面積を S(x, r) とする。 このとき M
が向き付け可能で compact であるとし, もしも M のすべての点 x に於て充分小さい r に対して常に
1. S(x, r) < πr2 ⇒ M は S2 と位相同型。
2. S(x, r) = πr2 ⇒ M は T2 と位相同型。
3. S(x, r) > πr2 ⇒ M は g 人乗り浮き輪 (g ≧ 2) と位相同型。
昔, Grothendieck の代数幾何の講義に出たことがあるが, 最初から最後まで古典代数幾何の話だった。
彼はイタリア学派の代数幾何を非常に良く理解し, そして Weil の Foundations (of algebraic geometry, AMS,
1946) を完璧に理解していた。
或るアメリカ人数学者 (朝倉政典: 数論幾何学
大学で学ぶ数学 part 2
数学セミナー (1) 2004)
Saturday, 21st February, 2004.
反応拡散方程式 [Alan Mathison Turing (1912 -- 1985)]
∂u/∂t = f(u) + D∇2u,
(t: 時間, u: 物質の濃度, f: 反応速度, D: 拡散係数)
この式が受精卵から複雑な身体が出来るのが, 反応拡散によって蛋白質などの濃度のむらが生じ, それが細胞に異なる変化を起こす結果であると Turing
は主張した。 実際シマウマの縞, 蛙の斑点, 豹の網目, タテジマキンチャクダイの縞模様, 等々の縞模様 [近藤滋: 生物の形態形成の化学的な基礎, 1952]
や, 胎児の指の形成 [三浦岳], 神経系の情報伝達 [三池秀敏] がこの方程式で説明されるという。
動物達の模様を解く魔法の数式
シマシマ, ボチボチ, アミアミ...自在
天才数学者が残した遺産
科学 ウイークエンドサイエンス & テクノロジー
朝日新聞, evening, Saturday, 14th February, 2004.
(Turing, A. M., The chemical basis of morphogenesis, Phil. Trans. Roy.
Soc. London B237 (1952), pp. 37--72.)
[7 の倍数判定法]
「数学質問箱」 の掲示板で 7 の倍数判定法を尋ねている人がいた。
「考える人」 氏は基本的に 1999 年の column に出ているのと同じ方法, 即ち 1000x + y = (1001 - 1)x + y ≡ -x +
y (mod 7) を用いていた。 「ガウディ」 氏は初めて見る方法, つまり x - 2y = (21 - 20)x - 2y ≡ -20x - 2y =
-2(10x + y) (mod 7) を用いていた。 ここで mod 7 は zero divisor を持たないので, 「ガウディ」 氏の方法では 7
の倍数であることは判定出来るが, そうでないときの余りをだすのは面倒である。
先ず例えば 1700412 を 「ガウディ」 氏の方法で判定してみると: 170041 - 2・2 = 170041 - 4 = 170037 → 17003
- 7・2 = 17003 - 14 = 16989 → 1698 - 9・2 = 1698 - 18 = 1680 → 168 - 0・2 → 16 -
8・2 = 16 - 16 = 0 だから 7 の倍数である。 一方これを 「考える人」 氏の方法と 1999 年の column で述べた倍数判定法
(2, 3, 1 則) を併用してみると, 1 700 412 ≡ 1 - 700 + 412 = -287 = -(2・2 + 3・8 + 7) ≡ -(4
+ 3) = -7 ≡ 0 (mod 7).
次に 318765 でやってみよう。 318765 = 7・45537 + 6 だから割りきれないはずである。 実際, 「ガウディ」 氏の方法では
318765 → 31876 - 5・2 = 31876 - 10 = 31866 → 3186 - 6・2 = 3186 - 12 = 3174 → 317
- 4・2 = 317 - 8 = 309 → 30 - 9・2 = 30 - 18 = 12 (≡ 5 (mod 7)) は 7 では割り切れない (が余りは
5 ではない)。 又これを 「考える人」 氏の方法でやると 318 765 ≡ -318 + 765 = 447 ≡ 2・4 + 3・4 + 7 ≡ 8 +
12 ≡ 1 + 5 = 6 (mod 7) で割り切れないことと, 余りが 6 であることが同時に判定出来る。
実は 「ガウディ」 氏の方法でも一寸工夫すれば, ちゃんと余りが求められる。 先ほどの 318765
でやってみると, -2(10x + y) の -2 ≡ 5 (mod 7) の逆数を求めなければならないのだが, 5・3 = 15 ≡ 1 (mod 7)
だからそれは 3 であることが分かる。 318765 を 12 ≡ 5 (mod 7)) に変換するまでの変換回数 (→ の数) を数えると, 4 回だから,
最後の 12 ≡ 5 (mod 7)) に 3 を 4 回掛けて 7 で割った余りを求めれば良いことが分かる。 実際 34・5 = (32)2・5
≡ 92・5 ≡ 22・5 = 20 ≡ 6 (mod 7) でちゃんと余りが求められている。
Wednesday, 11th February, 2004.
I. Porteous (ポータス) は, 臨界点 (極大点, 極小点, 変曲点) や特異点の様に, 他の点と異なる特徴を持った目立つ点のことを
Landmark points (ランドマーク点) と呼ぶことを提唱した。
曲面の縮閉面を考えると, 臍点が Thom の catastrophe 理論に於ける pyramid, 財布に対応している。
多様体 M 上の点 p を通る曲率線 γ(t) (γ(t0) = p) と, それに沿った主曲率 κ(t) が, κ'(t) = 0
を満たすとき, p は M の峰点と呼ばれる。
Paul Painlevé (1863 -- 1933) は世界で初めて飛行機に乗って空を飛んだ数学者であるらしい。 Saturday,
10th October, 1908 Camp d'Auvours で Wilbur Wright (1867 -- 1912) に同乗。
飛行時間は一時間十分。
単射半径 i と直径 d に関する球面に対するブラシュケ予想: i(Sn, g) = d(Sn, g) = π
ならば g は定曲率 1 の標準的な計量である, は正しい。 特に, 実射影空間 RPn 上の SCπ-計量
(閉測地線が単純であり, 多様体上の任意の測地線が周期 π で方向まで含めて元に戻る閉測地線であるという性質を持つ計量) は標準的な定曲率 1 の計量に限る。
[Berge]
これの証明は vol(M, g) ≧ (i(M, g)/π)nvol(Sn, g0),
等号成立は (M, g) が定曲率 Riemann 計量を持つ Sn の時でその時に限る, を用いる。
[有限増分不等式]
区間 I 上の連続函数 f が I を含む開区間で微分可能ならば, x, a ∈ I に対し
|f(x) - f(a)| ≦ |x - a|supt∈I|f'(x)|
が成立する。
[補題] 有限区間 [a, b] で連続な実数値函数 f が [a, b] を含む開区間で微分可能で, 且つ導函数 f' について f'(x) < M on
[a, b] を満たすならば f(x) - f(a) ≦ M(b - a)
補題の証明: E = {x ∈ [a, b]| f(x) - f(a) ≦ M(x - a)} という集合を考える。 明らかに a はこれを満たすから,
空集合ではない。 この上限 p = sup E を採ると, f の連続性から f(p) - f(a) ≦ M(p - a) を満たす。 従って p = b
ならばそれで終わりである。 もしも p < b であるとするならば, f'(p) < M が仮定だから, p < q < b であるような q が存在して
f(q) - f(p) < M(q - p) を満たすが, f(q) - f(a) = (f(q) - f(p)) + (f(p) - f(a)) < M(p
- a) + M(q - p) = M(q - a) が成り立って矛盾。
これから有限増分不等式が言える。
[系] 上記と同じ仮定で |f(x) - f(a) - f'(a)(x - a)| ≦ |x - a|supt∈I|f'(x) -
f'(a)|. (上の不等式で f(x) - f'(a)(x - a) を適用) [梅田亨, 数学セミナー (1), 2004]
有限増分不等式は, 凸開集合 D を採り, f'(x) ∈ D on [a, b] ⇒ f(b) - f(a) ∈ D ̄(b - a) (D ̄ は D
の閉包)
当たり前のことを言うようだが, 数学の問題には難しい問題もあれば簡単な問題もある。 数学教育をする上では,
簡単な問題から難しい問題へと問題を配置することが望ましいということは, 別に数学教育に携わっていなくても想像が出来るだろう。
ところが, じゃぁ何が難しくて何が簡単か, というのを判定することはとても難しいことである。 例えば三次函数の graph を描こうと思うと,
先ず微分して因数分解し, 導函数の零点を求めてcritical value (つまり導函数の零点での元の函数の値) を求め, 増減表を書き...
という作業をするが, この因数分解と零点を求めるというのが曲者だったりするからだ。 つまり普通 y' = 3x2 - 12x + 9 =
3(x - 1)(x - 3) で零点は x = 1, 3 というのと, y' = 3x2 + 6x = 3x(x + 2) で零点は x
= 0, -2 というのだと前者の方が後者よりも難しいと思うのだが, そうではなくて後者の方には x が単独因数として出て来る困難と, その単独因数が x =
0 という零点を生むことの困難と二つがあって, 学力の低い人間にはずっと難しい問題であったりするのだった。
このように, ある問題の困難の程度というものは, 他人からみて測ることの出来ないものなのであった。
Sunday, 8th February, 2004.
前へ
次へ
コラムの墓場の目次へ
HOME
 図で一辺 1 の正方形 ABCD に, 頂点 A
を共有して内接する正三角形 APQ が描かれている。 この時 ∠BAP = ∠DAQ = 15°である。 以下ではこれを用いて 15°,
75°の三角比を高校一年生程度の知識で求める。
図で一辺 1 の正方形 ABCD に, 頂点 A
を共有して内接する正三角形 APQ が描かれている。 この時 ∠BAP = ∠DAQ = 15°である。 以下ではこれを用いて 15°,
75°の三角比を高校一年生程度の知識で求める。