�����̊�� �u�荠�ňՂ������́v �������o����� �u���w�G���v �̑薼�̉�, ���w����ʐM 2005 �� 52 ���v �Ɍf�ڂ��ꂽ�B
Monday, 17th November, 2003 �� 40 �Ԗڂ̃����Z���k�f�� (Mersenne prime): 220996011 - 1 ���������ꂽ�B 6320430���B �~�V�K���B�����w�@�ʼn��w�H�w���U����}�C�P���E�V�F�[�t�@ Michael Shafer �������B
Saturday, 13th December, 2003.
2��2 �� 2.6651441426902251886502972498731 �Ƃ������� Hilbert �̒��z���ƌĂ�Ă��邻���ł���B
Sunday, 7th December, 2003.
���鎎�s�̌���, ���� A ���N����m���� p (0 < p < 1) �Ƃ���B ���̎��s�� n ��Ɨ��ɍs���Ƃ�, A �̋N����� Sn
�Ƃ����, Sn/n �� p as n����. �����������m�Ɍ�����, |Sn/n - p| > �� �ƂȂ��m����
n �� �� �̎� 0 �Ɏ�������B [Jacob Bernoulli �̒藝]
�@���̒藝��, Jacob Bernoulli �͓��z���ڂ����v�Z���邱�Ƃɂ���ďؖ����� (�������r, �m���_, �։ؖ[)�B
�@Bernoulli �̒藝��, ����m���_�ɉ��Ă�, ���̑吔�̎�@���ƌĂ��藝�̓��ʂȏꍇ�ɂȂ��Ă���:
�m���ϐ��� {Xi}i=1n �͓Ɨ������z�Ŋe Xi �͕��ς� m �ł���Ƃ���B ���̎�
�̓� > 0 (limn���� P(|(��i=1n Xi /n - m| > ��) = 0).
����, �� i ��ڂ̎��s�Ŏ��� A ���N����Ƃ� Xi = 1, �N����Ȃ��Ƃ� Xi = 0 �Ƃ���� P(Xi = 1) = p, P(Xi = 0) = 1 - p. E(Xi) = p, Sn = ��i=1n Xi �ł��邩��B
���c�m
�吔�̖@��
���w�Z�~�i�[ (11), 2003
�u�Z���g�E�y�e���X�u���N�̖��v �Ƃ����̂�����B ����� �u�d�݂𓊂������� i ��ڂɏ��߂ĕ\���o����܋� 2i �~�����v
�Ƃ����q�̊��Ғl�Ɋւ�����ł���B �ui ��ڂɏ��߂ĕ\���o��v �Ƃ����m���� 1/2i �ł��邩��, ���̊��Ғl�� ��i=1�� 2i/2i =
�� �ɂȂ��Ă��܂��B �Ƃ������Ƃ�, ���̓q�ɂ͎Q���������ł����Ă���ΎQ�������������Ƃ������ƂɂȂ�B
�@��, ���͎��̂悤�Ȏ�@�������藧�̂ł���Ƃ����B
�� i ��ڂ̓q�̏܋��� Xi �Ƃ����,
�̓� > 0 (limn���� P(|(��i=1n Xi /(n
log2n) - 1|
> ��) = 0).
�@����ɋ����, n �����̓q�ɒ��킷���, ���ϓI�ȏ܋����z�� n log2n �~�Ƃ������ƂɂȂ�B
Ibid.
A. A. Markov (�}���R�t, 1856 -- 1922) �� 1906 �N�̘_���� �u�G�t�Q�j�[�E�I�l�[�M���v ��@�u���p�O���t�̗c�N����v
���̕��w��i�̒��ł̕ꉹ�Ǝq���̌�������ɂ���, ���̂悤�Ȗ͌^���Ă����B
�@�L���W�� S = {a1, a2, ..., aN} ���̂�, ���� n + 1 ���̒���
�� �Ƃ��̙p�W�� 2�� ���l��, ���̏�Ɏ��̏��������m�� P �����߂�:
��b(k) �� S (P[x(k) = b(k), k = 0, 1, ..., n] = p(b(0))�Ep(b(1), b(2))�cp(b(n-1),
b(n)), where
p(ai)) �� 0 for i = 1, 2, ..., N;
P(a(i), a(j)) �� 0 for i, j = 1, 2, ..., N;
��k=1Np(a(k)) = ��k=1Np(a(i), a(k))
for i = 1, 2, ..., N.
�@���̊m�� (���͊m���ϐ��� {x(0), x(1), ..., x(n)} �� �� ) ���������z {p(a(i))} ��, ����̐��ڊm�����s�� (p(a(i),
a(k))i, k = 1, 2, ..., N �ŗ^�������ԋ�� S ��̃}���R�t�n��Ƃ����B
�r�c�M�s
�m���ϐ���m���ߒ���
���w�Z�~�i�[ (11), 2003.
(�O�l�W�F���R, �q���`��, �m���_����, �݂����̕t�^�Q��)
���S�Ɍ��藝�ƌĂ���ނ̒藝�����邪, ���̖��t���e�� G. Polya (�|�[��, 1887 -- 1985) ��, 1920 �N�̂��Ƃł���Ƃ����B
�r�c�M�s
�m���ϐ���m���ߒ���
���w�Z�~�i�[ (11), 2003.
���w�̑̌n�Ƃ��Ă̊m���_��, �w��㐔�w�Ɠ����悤��, �����n���猵���ɍ\�������K�v������, ���̎��͉\�ł���B (����) �m����Ԃ�������������W���n�Ƃ��Ē�`����B ���̏W���������Ӗ����Ă��邩�Ƃ������Ƃ�, �m���_�������Ɏ�舵���ۂɏd�v�Ȃ��Ƃł͂Ȃ� (Hilbert �� �u�w�̊�b�v �Q��)�B �ǂ��m���Ă���悤��, �S�Ă̌����I�� (���ۓI��) ���_��, ������Ȃ���̓I�ȉ��߂����������̂ł���B ���̂悤�Ȃ킯��, ���w�I�m���_�����ꂼ�ꎩ�g���琶������߂ƕ���ő����̉��߂��������B �]����, ���̌�̖{���̈Ӗ��ł͋��R���ۂ�m���̊T�O�ƊW�Ȃ��悤�ȉȊw�̗l�X�ȕ���ɂ����w�I�m���_�����p�����̂ł���B
�R�����S���t, A. N., ���{�L�i��
�m���_�̊�b�T�O
�����}��, 1975.
Monday, 3rd November, 2003.
Bertrand (�x���g����) ��paradox
�@�����, �~�������Ă�������钼�����l����B ���̒������~�ɂ���Đؒf����钷����, �~�̓��ڎO�p�`�̈�ӂ̒�����蒷���m���͊���Ƃ������B ���ꂪ
paradox �Ƃ�����̂�, �F�X�Ȗނ������Ȋm���������邩��ł���B
�@���͐��w�Z�~�i�[�ŏ��߂Č����B ���������� (3), 1980 ��������������Ȃ������̂���, ����Ȃ̂��ǂ����s���B ���e�ɂ��Ă͓��{�ꂾ��
http://www.nikonet.or.jp/spring/katudou/katudou.htm
http://www.comm.musashi-tech.ac.jp/~arimoto/arimoto/random/random.htm
�̈�ԉ����B �p�ꂾ��
http://www.cut-the-knot.org/bertrand.shtml
http://www.math.uah.edu/statold/buffon/buffon3.html
http://web.mit.edu/tee/www/bertrand/
http://robotics.eecs.berkeley.edu/~wlr/126/bertrand.htm
http://mathworld.wolfram.com/BertrandsProblem.html
���B
�@�������}�g��w������ꍂ���w�Z�̖q���p�����ɂ��ΐϕ��w�̊�b�T�O�ł����l�Ȓ����Ƃ������̂��`����� 1/2 �ɂȂ�Ƃ����B(�������傤���w����
No. 47)
�@Bertrand �������ɂ�, �l�X�Ȋm���������邪, �ǂꂪ�������������肷��̂͐��w�̖��ł͂Ȃ��B �e�X�̊m�����Z�o�����Ƃ��ɂ�,
���̊e�X�̊m���̍����ɂȂ��Ă��鉼��Ƃ������̂�����B �܂肻�ꂪ�����������ɂ���ċ��߂���m�����������B �������ǂ̉��肪��������,
�Ƃ������͐��w�ł͂Ȃ�, ���w�͂��̉���ɏ]���Čv�Z����ߒ��ɂ���, �Ƃ����̂ł���B
�@����, �����w�Z�̐��w�ň����Ă���m���̖��₻�̑��̕���̏������p��� (���͑�) �̌ӎU�L���Ƃ����̂�, �ǂ������̕ӂɂ���悤�ȋC������̂ł���B
Saturday, 4th October, 2003.
Yahoo ! �̐��w�f���� arith_in_cript �Ƃ����l�������Ă�����:
1 + 2 + (3 + 4 - 5)/(6 - (7/8) + 9) = 3.1415929...
Saturday, 27th September, 2003.
��r=0n (nCr)2 = 2nCn
�ł���Ƃ����̂͗L���Șb�� (1 + x)n(x + 1)n = (1 + x)2n �� xn
�̌W�����r���邱�Ƃɂ���ďؖ������B
�@�ł� ��r=0n (nCr)3 �͂Ƃ�����,
���͂��܂�悭�������Ă��Ȃ��B ���̐���
Franel numbers �Ƃ����B ���̐��Ɍ��炸,
�W�����݂̘a�ł͕������Ă��Ȃ����Ƃ������悤�ł���B
Saturday, 6th September, 2003.
Cauchy �̑��藝�ł���, ����͊��m���֏o������Ƃ� (�ǂ�ȂɍT���߂ɉ]���Ă����Ȃ��Ƃ����̖{���I�ȕ�����), ���Ȃ��ł��Ă��܂��悤�Ȃ��̂ł��B �����]���ƍ����̉䂪���̐��w�ҒB�͒���, �ł͋l�܂�Ȃ��̂�, �Ǝv���Ă��܂��悤�ł���, �}�����̔��ł�����, ���̉Ȋw��������藝�����������Ƃ�������, ����͎��R�����������Ȃ������Ƃ����猈�܂��ċ������� (���ꂪ��������邩�ۂ��͕ʂƂ���) �ł���, �]�͂ΐ��̓��ݓI�����Ƃł��]���ׂ����̂ł���, ���̎����͗Ⴆ��₵�ċ��ٓI�ł��B�Ɖ]���܂��̂͌`���I�_���̓���\�z�o���Ȃ��悤�Ȃ��̂ł���܂����, ���̌`���܂��ƂɊȒP�ł����� flexible �ł�����, ���ɂ��g�������Ɏv���邱�Ƃł� (���ۂ����Ȃ̂ł���)�B
����
���_�̍u�`�m�[�g, 1953
�u�������v �Ƃ����T�O�������̂̓��n�l�X�E�P�v���[�ł���Ƃ����B
��_��
�J���@���G���̌����Ƃ��̌n��
���w�Z�~�i�[ (9), 2003.
�J���@���G���̌����� �u�s���ʂ̊w�v Geometria Indivisibilibus Continuorum Nova quadam ratione promota, 1635 �̑� VII ���藝 I ���� I �Ƃ���
�������s���̊Ԃɍ��ꂽ�C�ӂ̕��ʐ}�`��, ����, ���̕��s�����瓙�����̂Ƃ���ň����ꂽ���ʐ}�`���̔C�ӂ̒����������������Ȃ��, �݂��ɓ������B ������, �������s���ʂ̊Ԃɍ��ꂽ�C�ӂ̗��̐}�`��, ����, ���̕��s���ʂ��瓙�����̂Ƃ���ŕ`���ꂽ���̐}�`���̔C�ӂ̕��ʕ������������Ȃ��, �݂��ɓ������B
�Ƃ��ďo�ė���B
��_��
�J���@���G���̌����Ƃ��̌n��
���w�Z�~�i�[ (9), 2003.
Saturday, 30th August, 2003.
�֍F�a�ɂ��ď����ꂽ
page
�ɋ����, 1683 �N (Leibniz ��� 10 �N����) �ɂ͍s���l���Ă���, Bernoulli ���� Jacob Bernoulli
�����O�ɔ������Ă����������B ���f���̊T�O�͂Ȃ�������, �����̍�����������������, 1661 �N�ɒ����� Yank Hui
�̂��̂��������ē��{�ŏ��߂Ė����w�� 1683 �N�Ɍ��������B 1685 �N�ɂ� Horner �ɐ�邱�ƈꐢ�I, 30 + 14x - 5x2
- x3 = 0 ���������B ������ Newton(-Raphson) �@�������B
�@Bernolli ���Ȃ�Ăǂ�����Ĕ��������̂��낤�� ?
Sunday, 26th July, 2003.
��ABC ��, ���̎��㖔�͓����̓_ P �ɑ� L(P) = PA + PB + PC �ƒu���B AB �� AC �� BC �Ƃ���Ƃ� L(P) �� P = A �ōő�l���̂�B [Visschess, 1902]
�ؖ�: (Svetoshev Savchev, Titu Andereescu Mathematical Miniatures, The
Math-Ass. of America, Anneli Lax new Math Library vol. 43, 2003 �ɂ��)
��ʂɕ��ʏ�̔C�ӂ̈قȂ��_ X, Y �ɑ���, ���� XY �̒��_�� M �Ƃ����, ���ʏ�̔C�ӂ̓_ P �ɑ� PM �� (PX + PY)/2
�����藧�B �A�������� P = X ���� P = Y �̎��Ɍ���B ����́�PXY �Ƃ���� M �𒆐S�� 180
�x��]���������̂Ƃō���镽�s�l�ӌ`���l���Ă݂�Ε�����B ���̎�����
AM �� (AX + AY)/2, BM �� (BX + AY)/2, CM �� (CX + CY)/2
�Ȃ̂ŕӁX����, s(P) = AP + BP + CP �ƒu���� s(M) �� (s(X) + s(Y)) ��B ��, ���� XY ���, �O�_ A, B, C �������ɂ��邱�Ƃ͂Ȃ��̂����瓙���͐������Ȃ��B ����
s(M) < (s(X) + s(Y))
���� s(P) �͘A�������Ł�ABC �͗L�E�̈悾����ő�l������, s(M) < s(X), s(M) < s(Y) �ł��邩�� s(M)
�͍ő�l�ł͂Ȃ��B ���E���܂߂���ABC �ɓ���ǂ̂悤�Ȑ��� XY �Ɋւ��Ă����̂��Ƃ���������̂� s(P) �́�ABC �̓����ōő�l���̂蓾�Ȃ��B
(���̏ؖ�����O�p�`�łȂ��Ă��ʑ��p�`�ł������ł͍ő�l���̂�Ȃ����Ƃ�������)
�@����, ��ʂɁ�ABC �� AB �� AC �� ��B �� ��C �ł���B P �� AB ��ɂ���Ƃ���� PC �� AC �ƂȂ邩�� L(P) = (PA +
PB) + PC �� AB + AC, P �� AC ���� BC ��ɂ���Ƃ������l�ł���B ��� L(A) = AB + AC �ł��邩�� L(P) �� P
= A �̎��ɍő�l���̂�B
Sunday, 20th July, 2003.
�����Ɋ��ł��߂������������݂���, �Ƃ����͎̂����ł�����, �Ⴆ�� m, n �𐮐� (n >> 1), 0 < b < 1 �Ȃ� (�L��) ����, ������ c ��p���� m �} bnc �Ƃ����������Ηǂ��B ������ Pisot number �Ƃ��Ēm����悤�Ȃ��܂莩���Ƃ͎v���Ȃ��悤�Ȑ���, ���Ȃ萮���ɋ߂������������݂���B (���ɂ�����������B)
{an} �� Lucas ����Ƃ��悤�B ���� a1 = 1, a2 = 3, an = an-1 + an-2. ���L�̂悤�� Fibonacci ����� {Fn} �Ƃ����, an = Fn+1 + Fn-1 �ł��邪, p ��f���Ƃ���Ƃ� ap �� 1 (mod p) ���������� [Lucas ����̊�{�藝]�B
Fibonacci ���� {Fn} �̋t���`�̘a�Ɋւ��Ă͔��ɕ��G�ȋ���������:
��n=1�� 1/(FnFn+2) = 1.
��n=1�� (-1)n-1/(FnFn+1) =
(��5 - 1)/2.
��n=1�� 1/(F2n+1 + 1) = (��5)/2.
��n=1�� 1/(F2n) = (5 - ��5)/2 [Lucas, 1878].
(����� F �̔ԍ��� 2n �ł���)
��n=1�� 1/F2n = (��5)(L(1/��2) - L(1/��4)),
�A��, �� = (1 + ��5)/2, L(q) =
��n=1�� qn/(1 - qn) �̓����x���g���� [�J�^����,
1878]
��n=1�� 1/F2n-1 = (��5)��22(1/��2)/2,
�A�� ��2(q) = 2q1/4��n=1�� qn(n-1)
�� Jacobi �� �� ���� [Landau, 1899]
�@��n=1�� 1/Fn = 3.359885662... �͖������ł��� [�A���h���W���j��,
1989; �u���V���[ & ���@�[�i�l��, 1994; �h�D���F���l, 1997] �����z���ł��邩�㐔�I���ł��邩�͕s���ł���B
�h�D���F���l�̏ؖ��ɂ��Ă͐��w�Z�~�i�[ (7), 2003 �̉���F�����̋L���ɏo�Ă���B ��,
��n=1�� 1/Fn �̖������̏ؖ��@�ɂ��,
��n=1�� 1/F2n �̖�������������B
�@��n=1�� 1/F2n-1,
��n=1�� 1/Fn2, ��n=1�� 1/Fn4,
��n=1�� 1/Fn6, ... �͒��z���ł��� [�h�D���F���l, �����[��, �����v
���q& ����,
1996] ��,
��n=1�� 1/F2n ���㐔�I�����z�I���͕s���B �X�� ��n=1�� 1/Fn3,
��n=1�� 1/Fn5, ��n=1�� 1/Fn7,
... �͖��������ǂ������s���B
�@�C�ӂ̐��� a �� 1, b �� 0 �ɑ��� ��n=1�� 1/Fan+b �͖������ł���
[�}�^���A�z-�v���{, 2002 (a, b ���݂��ɑf�̏ꍇ), ���J�m��, 2003 (���)]
�@��n=1�� (-1)n/(F2n) �͒��z��
(subscript �� 2n) [�u���V���[-�y�e, 1987]
�@���� a �� 1, b �� 0, d �� 2 �ɑ� (d = 2 & b = 0 �̏ꍇ������) ��n=1�� 1/Fadk+b
�͒��z��, ���O����鐔�� ��n=1�� 1/F2ka = 1/Fa
+ (��2 + 1)/(��(��2a - 1)) (�� �͏�L�Ɠ��� (1 + ��5)/2) [�x�b�J�[-�e�b�p�[,
1994]
�@���� a �� 1 ���Œ肵, �W�� {��n=1�� 1/Fadk+b},
���� b �� 0, d �� 2 �� d = 2 & b = 0 ������, �͑㐔�I�Ɨ� [�����v���q-�c���F��-������, 1999]
�@��n=1�� 1/FFn �͒��z�� [�c���F��, 1999]
�@d �� 2 �͐���, an, bn �͐������ an �͖��������ł͂Ȃ�, ������ limn����
(log(max(1, |an|)))/dk = limn���� (log(max(1, |bn|)))/dk
= 0 �Ƃ���� d = 2, an ���萔�� bn ������ԍ��ȏ���łȂ��ꍇ ��n=1��
an/(Fdn + bn) �͒��z���ł���B �����O�������͓� Q(��5)
�ɓ��� [�h�D���F���l-�����v���q, 2003]
Saturday, 12th July, 2003.
��������ƁX �� �Ə����̂�, �p���e�m���_�a�Č����������Ƃł��L���Ȓ����ƃt�B�f�B�A�X�Ɉ��� �u�t�B�f�B�A�X�̔�v �Ƃ��Ă�邩�炾�Ƃ����B ��������� �� �Ə������Ƃ�����̂� �u�����v ���Ӗ�����M���V���� (�у̓�ή ?) �̓������������ł���B (�� pi �� �� phi �͉������Ă���Ƃ�, Fibonacci �̓��������Ƃ�������������B Earliest Uses of Symbols for Constants ���Q�ƁB Saturday, 27th September, 2003 �ɉ��M)
�t�B�{�i�b�`����� {Fn}, F1 = F2 = 1, Fn+2
= Fn+1 + Fn �Ƃ���Ǝ��̊W�������藧��:
Fn+1Fn-1 - Fn2 = (-1)n
[�J�b�V�[�j-�V���\���̒藝�n
Fn2 + Fn+12 = F2n+1
Fn+m = FmFn+1 + Fm-1Fn
��k=1n Fk2 = FnFn+1
��k=12n-1 FkFk+1 = F2n2
��k=0n nCk Fk = F2n
Fn+k2 - (-1)k Fn2 = FkF2n+k
[Sharpe]
Saturday, 28th June, 2003.
�t�B�{�i�b�`�Ƃ��Ēm����s�T�̃��I�i���h��, �L���X�g���k�ŃA���r�A�������ŏ��Ɏg�����㐔�w�҂Ƃ������Ă���B
Wednesday, 25th June, 2003.
���f���� C �� n �����R�� (���̐���) �Ƃ��� x1/n �ɂ�� �`���I�p������ C[[x1/n]] �̏��� C((x1/n)) ���l����B ���̎� x1/1 = x, (x1/rn)r = x1/n �Ƃ����W�����藧���Ƃɂ�, �����̂悤�� xm/n = (x1/n)m �Ə������Ƃɂ��悤�B ���̎� C{x} = ��n=1�� C((x1/n)) �̗v�f���p���� fractional power series, ���� Puiseux �����Ƃ����B C{x} �͍\���@���璼���ɑ̂ł��邱�Ƃ������邪, ���͑㐔�I�̂ł�����B ���̏ؖ��� Newton ���p�`�Ƃ������̂�p���čs����B
Wednesday, 4th June, 2003.
[Euler �̒藝]
F(x) = F(x1, ..., xm) ��, �ϐ� x1, ..., xm
�Ɋւ��� n ��ꎎ��� (homogeneous polynomial) �ł���Ƃ�
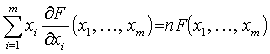
�X�Ɉ�ʂ�
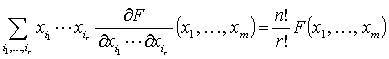
�ŏ��̎��̏ؖ���, F(x) �� n ��ꎎ����ł��邩�� F(tx) = tnF(x) �ƂȂ�̂�, ���̗��ӂ� t �Ŕ��������
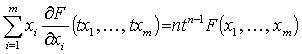 �ł��邩��, ����� t = 1 ��������Ɠ�����B
�X�� r �K�܂� t �Ŕ������Ă��� t = 1 ��������Ύ��̎���������B
�ł��邩��, ����� t = 1 ��������Ɠ�����B
�X�� r �K�܂� t �Ŕ������Ă��� t = 1 ��������Ύ��̎���������B
���̎����̂͑㐔�̕���ł͗ǂ��m��ꂽ�����炵����, �ؖ����@�Ɉꐡ���������̂ōڂ��Ă����B
Friday, 30th May, 2003.
Mordell-Weil �̒藝�ɂ���, Q ���`���ꂽ�ȉ~�Ȑ� E �� Q �L���_�̑S��
E(Q) �͗L������ abel �Q�ł���B ���� E(Q) = E(Q)tor�~Z r
�ƂȂ�B Mazur �̒藝�ɂ���� torsion �Q E(Q)tor �͎��� 15
�ʂ�̂����̉��ꂩ�ɂȂ邱�Ƃ��m���Ă���:
Z/nZ, 1 �� n �� 10 ���� n = 12,
Z/2Z�~Z/2mZ, 1 �� m �� 4.
�@�Ƃ����, Z r �̕��� r �̂��Ƃ�, ���̑ȉ~�Ȑ� E �̊K�� rank �Ƃ����̂���, rank r
�ɂ͏�����Ȃ�, �܂�ǂ̂悤�Ȑ��� n ���l���Ă�, ������� rank �̑傫���ȉ~�Ȑ� E �����݂������ʂɐM�����Ă����B
�@�ł͌��݂ǂ̈ʂ� rank �̑ȉ~�Ȑ����m���Ă��邩�Ƃ�����, �ӊO�ɏ����� rank �������m���Ă��Ȃ��B ���݂̂Ƃ���ő�� rank ��
Martin-McMillen (2000) �ɂ�� rank �� 24 �Ƃ������̂ł���B ���S�� rank ���������Ă�����̂� Dujella
(2001) �ɂ�� rank = 15 �Ƃ������̂ł���B ������ rank �͂��̂悤�ɓɂ����B���Ă��Ȃ���, �ȉ~�Ȑ��̌W���̕��͉��� 58
���ɂ��y�ԑ傫�����ł���B �����̋L���� Andrej Dujella ������ page �ɋ����Ă���B
Saturday, 24th May, 2003.
Miles Reid (�}�C���X�E���[�h) ����, ���̒��� Undergraduate Commutative Algebra (�M�� �u���_����v �ɓ��R������, ��g���X) ��, �㐔�w�����ۉ������������Ƃɂ���, ���̂悤�ɏq�ׂĂ���:
�㐔�w�����̐��w���瘨����������, ��ʂ̊w�����ɋ�����ۂɒ��ۓI�� approach �����ł͕s�\���Ȃ��Ƃł���B �O�҂͒P�ɍl�����̖��ł���B ���͑㐔�w�� seminar ��, ���̓��������̌���, �p��, ���ʂ̔���, �Đ��Y�̋@�\�ɂ����, �Q�b�g�[�̂悤�ȕ��Љ���`����, ���̕���̓����ɋ���������Ȃ��悤�ɂ��Ă��邱�Ƃ��c�O�ł���, �s���S�ł���Ǝv���B
�� 9 �� ���悤�Ȃ� !
9.8 ���j���������
���͂���� �u�㐔�w�v �𐔊w�ɒ���, �u���̐��w�v �� �u���̊w��v �ɓǂݑւ��������ǂ��Ǝv���B
���z�@���ɂ͓�ʂ肠���� a(b + c) = ab + ac, (a + b)c = ac + bc �Ȃ̂���, �ǂ��炩���E���z�@�� (right-distributive law) �łǂ��炩�������z�@�� (left-distributive law) �ƌĂ��B �����ǂ������ǂ��������Y���B ������ Internet �Ō������Ă݂���, ������������ site �ł͉E���z�@���ƌĂ�, �ʂ� site �ł͍����z�@���ƌĂ�Ă���̂������B ��������͎̂������ł͂Ȃ��ƒm���Ĉ��S��������, �{���ɐ������̂͂ǂ������ǂ����Ȃ̂��낤 ?
�ꎟ�ϊ��Ƃ����̂͗ǂ��m���Ă��邪, ���႟�ϊ����Ă����̂͂���̂��낤�� ? �Ƃ����̂��ȑO�����ꂽ�B ���͂���̂ł���B P2(C)
���� P2(C) �ւ̑o�L���ʑ� birational mapping
(�����ł�ꎎ����W�ŕ\���Ă���)
�� (x0 : x1 : x2) = (x1x2
: x2x0 : x0x1)
��ϊ� quadratic transformation ���� Cremona �ϊ��Ƃ����B
�@���̎ʑ��̐�����, ��쌒���� �u�㐔����v ��g���X, 1995 ��������Ղ��B ���̖{��, �����I�ȋ�̗�ɏڂ�����,
�㐔�̓���Ƃ��Ă͗ǂ��{�ł���Ǝv���B
Wednesday, 21st May, 2003.
���시���`����Ƃ��� (���w�Z�~�i�[ (6), 2003) �ɂ���, abelian group �Ƃ������O���ŏ��ɗp�����̂� Jordan �ł��邪, ����� symplectic group Sp(n, Fp) �Ƃ�������Q�ł������B ���݂̂悤�ɉ��Q�̈Ӗ��� abelian group �Ƃ������t��p�����̂� Kronecker �ł�����, Abel �������ɕt��������Q�̂��Ƃ��������̂ł������B Kronecker �����Ȃ����, symplectic group �͍��ł� abelian group �ƌĂ�, ������������ Sp �Ƃ����L���̑���� Ab(n, Fp) �Ƃ����悤�ȋL�����p�����Ă�����������Ȃ��B
Wednesday, 14th May, 2003.
�W���� ![]() �Ə����悤��, �����W��
multinomial coefficient ��
�Ə����悤��, �����W��
multinomial coefficient �� 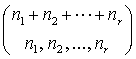 �Ə������V������悤���B
�Ə������V������悤���B
Saturday, 26th April, 2003.
�Ȑ� (�~���Ȑ�) �� pencil (pencil of conics) �Ƃ����̂� conic bundle (�~���Ȑ���) �ƌ����̂��������B ��, ���w�������悤�� �u�]��̂��銄�Z�v (�Ƃ����� �u�]����o�����Z�v) �͉p��� division with reminder �Ƃ��������ł���B
Sunday, 13th April, 2003.
{n! + k | k = 2, 3, ..., n} �Ƃ����W�����l����B ��, n > 5 �Ƃ���Ƃ��� n - 1 �̐��̒��ɑf���̗ݏ�͂Ȃ��B n �� 2 �ȏ�̎��R���Ƃ���Ƃ�, ���̌`�̐��őf���̗ݏ�ɂȂ�̂� 2! + 2 = 4 = 22, 3! + 2 = 8 = 23, 3! + 3 = 9 = 32, 4! + 3 = 27 = 33, 5! + 5 = 125 = 53 �����ł���B
��� ��
�K��͏���
���w�Z�~�i�[ (2), 2003, pp. 68--71.
Sunday, 6th April, 2003.
a, b �� b > a2 �������R���Ƃ���ƘA�����W�J
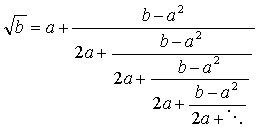
���o����B [���c�S�� (17��), ���w�Z�~�i�[ (3), 2003]
����, Riemann �ϕ��͏c�����, Lebesgue �ϕ��͉�����, �Ƃ����Ⴂ�����������B (����) �悸, �K�i�����ł�, �ǂ���ł������Ƃ������Ƃ����邪, ���� �u��l�����v �Ƃ����̂͂��Ƃ��� �u������v �̍l���Ȃ̂ł���B �������D�悷��ΕK�R Lebesgue ���ɂȂ�B Lebesugue �ϕ���, ��l�������痣��Ď��R�ɂȂ����̂ł͂Ȃ�, ��l�����ɗe�ՂɎ������߂鎩�R�Ȍ`�����l�������̂��B
�~�c��
�O����� ���x�Ɛϕ�
�L�E�����藝���߂�����
(5) ���W���Ƒ��x �� 4.
���w�Z�~�i�[ (3), 2003.
Tuesday, 1st April, 2003.
�kaplace �̎Z�p�I�m�� (Laplace �� �u�m���̉�͓I���_�v (1812 �N) �ɂ��)
�@�S�̂� n �ʂ�̏ꍇ������, ���̂���������l�Ɋm���炵���Ƃ���B ���鎖�� A �� �� �ʂ�̕��@�ŏo������Ƃ�, �` �̊m����, r/n
�ƒ�߂�B (http://www004.upp.so-net.ne.jp/s_honma/probability/probability.htm)
Monday, 31st March, 2003.
1, 1, 9, 9 �� 10 �������: (1 + 1/9)�~9 = 10.
[Wei-Hwa Huang �̖�� (3, 3, 8, 8 �� 24 �����) �̓�]
3!�~8 - 3�~8 = 24.
Tuesday, 25th March, 2003.
�u���w���┠�v �̌f���Ŏ��̂悤�Ȏ�����������B �ĊO�苭�������̂�, ���e�����ؖ� (�����I�ɏ������������������߂�) �Ƌ��ɂ����ɍڂ��Ă����B
0 < x < 1 �̂Ƃ����̕s����������: �� < sin(��x)/(x(1 - x)) �� 4.
tassui
2003/02/04(Tue) 02:25:37 No.665
�ؖ�: �悸 y = sin(��x)/(x(1 - x)) �ƒu���B
1) y �� x = 1/2 �Ɋւ��đΏ̂ł���B
�@����� x = 1/2 �} t �ƒu���đ�������, ����ɂ��Ă� -1/2 < t < 1/2 �� y = cos(��t)/(1/4 - t2) �ƂȂ邱�ƂŊm���߂���B
�@�]���Ĉȉ��ł� 0 < x �� 1/2 �Ƃ��ėǂ��B2) y �� 0 < x < 1/2 �ŒP�������ł���B
�@�悸 y' =(��cos(��x)�Ex(1 - x) - sin(��x)(1 - 2x))/(x(1 - x))2.
���� > 0 ������,
u(x) = ��cos(��x)�Ex(1 - x) - sin(��x)(1 - 2x)
�ƒu����, 0 < x < 1/2 �� u(x) > 0 �������悢�B �悸 u(0) = 0, u(1/2) = 0 ���ȒP�Ɋm���߂���B ����
u'(x) = sin(��x)�E(��2(x2 - x) + 2)
= sin(��x)�E(��2(x - 1/2)2 + 2 - ��2/4)
�� 0 < x < 1/2 �� sin(��x) > 0. ���p�̓s���� v(x) = ��2(x - 1/2)2 + 2 - ��2/4 �ƒu���B
v(0) = 2 > 0, v(1/2) = 2 - ��2/4 < 2 - 9/4 < 0.
������ v(x) --- �]���� u'(x) �� --- �� 0 < �� < 1/2 �ł��� x = �� �ɂ���� u'(��) = v(��) = 0 �ɂȂ�B ���̓_�� u(x) �͋ɑ喔�͋ɏ�����, x = 0, 1/2 �� u = 0 ������, 0 < �� < 1/2 �ƂȂ��� �� �Ɋւ� u(��) > 0 �Ȃ���͈̔͂� u(x) > 0, u(��) < 0 �Ȃ��, ���͈̔͂� u(x) < 0 �ł���B x = 1/4 �Ƃ����, u(1/4) = (3�� - 8)/(16��2) > 1/(16��2) > 0 ������ u(x) > 0.
�@�]���� 0 < x < 1/2 �� y' > 0 ������, y �͂��͈̔͂ŒP�������ł���B3) lim_(x��0) sin(��x)/(x(1 - x))
= �� lim_(x��0) sin(��x)/(��x(1 - x)) = ��
4) x = 1/2 �̎� y = 4.5) �ȏ�ɂ��
0 < x < 1 �Ȃ�� �� < sin(��x)/(x(1 - x)) �� 4.
Wednesday, 5th February, 2003.
�����Ɏ��̒藝�������ꂽ (���m�ɂ͈ꐡ�Ⴄ��)�B �ȑO��w�ő㐔�w 1 (����) �ŏo��������, �u�`�ŏo�ė��� Eisenstein (?) �� criteria ��p������ �u����Ȓ��w���ł��o����悤�ȏؖ���, ��藝���g���Ȃ��, �N�B�̌������^���v �݂����Ȃ��Ƃ����� �搶�Ɍ���ꂽ���Ƃ��v���o��...�B
�藝
�����W���� monic �ȑ㐔���������L�����������Ȃ�, ���̉��͐����ł���B
�ؖ�:
�^����ꂽ�������� xn + an-1xn-1 + an-2xn-2 + �c + a1x + a0 = 0 �ƒu���B ak �̑S�Ă� 0 �ł������Ƃ����, ���Ƃ̕������� xn = 0 ������, �����ȉ� x = 0 ���d���x n �Ŏ��̂�, ��ӂ����B �]����, ak �̂ǂꂩ�� 0 �łȂ��Ƃ���B
������ m = min{k | ak �� 0} > 0 �Ƃ����, ���Ƃ̕�������
xm(xn-m + an-1xn-1-m + an-2xn-2-m
+ �c + am-1x + am) = 0 �ƂȂ�̂�, �ŏ����� x = 0 �Ȃ���������Ă�����, a0
�� 0 �̏ꍇ�ɊҌ������B �]���Ĉȉ��ł� a0 �� 0 �Ƃ���B
������ xn + an-1xn-1 + an-2xn-2 + �c + a1x + a0 = 0 �̗L�������������� x = q/p, p > 0 �ƒu���B ��������
(qn + an-1qn-1p + an-2qn-2p2 + �c + a1qpn-1)/pn + a0 = 0
���� qn + an-1qn-1p + an-2qn-2p2 + �c + a1qpn-1 = a0pn.
p > 1 �Ɖ��肷���, ���̉E�ӂ� p �Ŋ��肫��邪, ���ӂ� p �Ŋ��肫��Ȃ��̂Ŗ����ł���B �]���� p = 1. ����ėL�������͐����� x = q �ł��遠
����: monic (�ō����̌W���� 1) �Ƃ��������͗��Ƃ��Ȃ� (�O�q�̓����͂���𗎂Ƃ��Ă���)�B ���̂Ȃ� 2x2 - 7x + 3 = 0 ���� (2x - 1)(x - 3) = 0 �̂悤�ȗႪ���邩��ł���B ���̘b���X�Ɉ�ʂɍL�����, �����W���� monic �ȑ㐔�������̉�S�̂�㐔�I�����Ƃ����Ĉ�̌�������ɂȂ��Ă���B
Sunday, 26 January, 2003.
���̎����͎��̌`�ɂ܂Ŋg���ł���B
A: UFD (= unique factorization domain), K: A �̏���, f �� A[x] �� monic �ȑ������Ƃ���B ���̎� a �� K: f(a) = 0 �� a �� A.
�@���̂��Ƃ͑��� UFD �� normal ring �ł���Ƃ������Ƃ��Ӗ����Ă���B
Wednesday, 14th May, 2003.
���, ����s����������, 2/11 �������ŕ\���K�v���������B ���ʂ̐l�͂ǂ���������Ȃ���, ���w�̐��Ƃ͂��̂��炢�͈ÎZ�ŏo����B ���� 2/11 = (2�~9)/(11�~9) = 18/99 = 0.18181818......
���̂悤�ɕ��ꂪ 999�c9 (= 10n - 1, 9 �� n ����ł���) �Ƃ����`�����Ă��镪����, �悸�ѕ����ɂ���, ���q�̌����� n ��菬������ΐ擪�� 0 �����Ă���, ���ꂪ�����_�ȉ��J��Ԃ����Ƃ�������������B �Ⴆ�� 12/999 = 0.012012012......
���ʂ̕��� �i����/���� �Ƃ����`����������) �͕K���z�����ŕ\����邩��, ����̐��� 2 �� 5 �������Ɏ����Ȃ���ΕK�����{������� 999�c9 �Əo����͂��ł���, 2 �� 5 �������Ɏ��ꍇ���l�����, ���ꂪ 2p5q �Ƃ����`�Ȃ� 999�c9000�c0 (= (10n - 1)10max(p, q), 9 �� n ���ё����� 0 �� p �� q �̏������Ȃ����̐���������) �Ƃ����`�ɏo����͂����B ���������ۂɊ��Z���ď����ɂ���ȊO�ł�, �ÎZ�ŕ�������̌`�Ɏ����ė����Ƃ����킯�ɂ͖w�ǂ̏ꍇ�����Ȃ��B �ܘ_���͂�����x�i���ė��� (�Ⴆ�� 1 �̈ʂ� 3 �������瑊��� 1 �̈ʂ� 3 �łȂ��Ɗ|�����Ƃ��� 1 �̈ʂ� 9 �ɂȂ�Ȃ��Ƃ������Ƃ͕�����), ������ȏ�͂قڂ���グ�ł���B �ÎZ����Ȃ���Γd���@�������������̂�, �d���@����, �d�삪�茳�ɂȂ���ΕM�Z����Ƃ������ƂɂȂ�B
�Ƃ����, 2/11 ���v�Z���������, ���q�͖Y��Ă��܂�����, 13 ���̊���Ƃ��������������ŕ\���K�v���������B ��قnj������悤��, ...3 �Ƃ��������|��������̂���, �\�̈ʈȏ�͊�ɂȂ邩������Ȃ� (���Ƃ��� 9 ������Ԃ�������Ȃ�)�B �Ƃ����킯��, �d����茳�ɂȂ������̂ŕM�Z�� (���̎��K�v�Ƃ���Ă���) ������ 2 �ʂ܂ŋ��߂��̂���, �ǂ����������B �A��̓�������F�X�l�����B
�m�� 7�~11�~13 = 1001 ������ --- ����� Cornelius Lanczos: Numbers Without End. �ēc�j�O�� �u���Ƃ͉����v �u�k�� Blue Backs #269 �ɏo�Ă����̂Ŏ��͗ǂ��o���Ă���̂ł��� --- 7�~13 �� 7�~3 = 21 ������ 91 ��, 11 �͌������炵�đ�������... �悵�悵, ������ 1001 �ɂȂ�B (����q�ׂ��悤��) 999�c9 = 10n - 1 �� 1001 = 103 + 1 �͐e�ʂ݂����Ȃ��̂������肭����������
1/1001 = (1/1000)�~1/(1001/1000) = (1/1000)�~1/(1 + 1/1000)
= (1/1000)�~(1 - 1/1000 + (1/1000)2 - (1/1000)3 + �c�c)
= (1/1000)�~((1 - 1/1000) + (1/1000)(1 - 1/1000) + (1/1000)2(1 -
1/1000) + �c�c)
= (1/1000)�~((1000 - 1)/1000)(1 + 1/1000000 + (1/1000000)2 + �c�c)
�Ƃ������Ƃ͗Ⴆ�� 352/1001 ����, ���q�� 352 �� 1000 �{���Ă��Ƃ̐��������� 351648 ��, ���ꂪ�����_�ȉ��z���邩�� 0.351648351648......
����Ȃ�قڈÎZ�ł���B ���Ȃ��Ƃ����Z��M�Z��������v�Z�ԈႢ�͏��Ȃ��͂����B
�Ⴆ��:
7/13 = (7�~7�~11)/(13�~7�~11) = 49�~11/1001 = 539/1001 = 0.538461538461......
3/7 = 3�~13�~11/(7�~13�~11) = 39�~11/1001 = 429/1001 = 0.428571428571......
�X�� a/11 (a �� 1 ���� 10 �܂ł̐���) �ł͂���� 9a/99 �ł���Ɠ����� 7�~13a/1001 = 91a/1001 ������, 91a �̕S�̈ʂ� �u��̈ʂ��� 1 �����������́v �͓������B �܂� Int(91a/100) �� a - 1 (mod 10) �ł���B �Ⴆ�� 8/11 = 56�~13/1001 = 728 ��, �S�̈� 7 �ƈ�̈� 8 ���� 1 �����������͓̂������B
Friday, January, 2003.
�O��
����
�R�����̕����ڎ���
HOME