2002 年の column
今朝の朝日新聞の Be という別刷りの紙面で, 毎週パズルがあるのだが, 今週は迷路とクロスワードだった。迷路の方だが, 最も単純な迷路は start と
goal が指定してあって, 真っ直ぐに抜ければいいのだが, この迷路は懸賞付きだということもあって,
通り抜けた未知の形を言葉で書かなくてはいけないようになっている。勿論単純に抜ければ, 形が浮き上がるようにはなっているのだが, かなり size がでかいので,
戦略として 「行き止まりの道」 を先ず塗りつぶしてから, 残りの道を進んでいくことにすると良い。このようにしていくと, かなりスイスイと進んでいけるが, 当然,
行き止まりの道を探すのに時間がかかる。
この迷路の攻略法でやっていくと, どうやら数学というのもこういう迷路に似ているなぁと思えてきた。一つの定理 --- それは数学的真理と言い換えても良い ---
を得るまでには, ああでもないこうでもないと, そっちの方面に進んでは成功しない行き止まりの道をあれこれと巡り, 一つ一つ 「ああこれは行き止まりの道だった」
と確認していく作業に似ている。そうして最後に唯々として正しい道に突き当たる。天才でない我々はこのようにして一つの定理を得たり,
或いは問題を解いたりしているような気がする。
Saturday, 21st December, 2002.
ポーカーの役の出現数
Friday, 20th December, 2002.
正多面体の中心を O, 一つの面の中心を C, その面の一頂点を A, それを橋とする一辺の中点を B, 面が正 p 角形, 頂点が正 q 角錐とするとき
∠BOC + ∠COA + ∠AOB = (10 - p - q)π/4.
一松信
公式 (11) p. 19 「高次元の正多面体」
日本評論社, 1983.
Saturday, 7th December, 2002.
a1 = p, an+1 = an(an - 2). [出題:
山内 暁]
解: [Tetsuya
Kobayashi]
an+1 = an(an - 2) = (an - 1)2
- 1.
∴ an+1 - 1 = (an - 1)2 - 2.
そこで an - 1 = bn + 1/bn と置くと
bn+1 + 1/bn+1 = (bn + 1/bn)2
- 2 = (bn)2 + 1/(bn)2.
従って bn+1 = bn2 はこの漸化式を満たす。 即ち
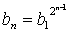 .
.
b1 + 1/b1 = a1 - 1 = p - 1. だから b12
- (p - 1)b1 + 1 = 0. 故に
b1 = (p - 1 ± √((p - 1)2 - 4))/2 = (p - 1 ± √(p + 1)(p -
3))/2.
よって
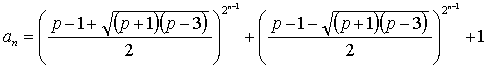
下で使っている
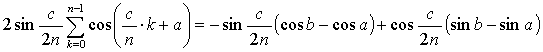
(但し c = b - a) の Euler の公式を用いない証明:
lhs = Σk=0n-1 sin(c/(2n))cos((c/n)・k + a)
= Σk=0n-1 (sin(c/(2n) + (c/n)・k + a) + sin(c/(2n) - (c/n)・k
- a))
= Σk=0n-1 (sin((c/(2n))(2k + 1) + a) - sin((c/(2n))(2k -
1) + a))
= sin(c/(2n) + a) - sin(-c/(2n) + a) + sin(3c/(2n) + a) - sin(c/(2n) + a) + … +
sin((c/(2n))(2n - 1) + a) - sin((c/(2n))(2n - 3) + a)
= - sin(-c/(2n) + a) + sin((c/(2n))(2n - 1) + a)
= -sin(a - c/(2n)) + sin( c - c/(2n) + a)
= sin(b - c/(2n)) - sin(a - c/(2n))
= sin b cos(c/(2n)) - cos b sin(c/(2n)) - sin a cos(c/(2n)) + cos a sin(c/(2n))
= rhs.
同様にして
2sin(c/(2n))Σk=0n-1 sin((c/n)・k + a) = -sin(c/(2n))(sin b
- sin a) - cos(c/(2n))(cos b - cos a)
が示される。 [これで高校生でも区分求積法で ∫ab sin x dx, ∫ab
cos x dx が求められることが分かった]
Friday, 6th December, 2002.
x > 0, y > 0, z > 0, 3x + 2y + z ≧ 12 ⇒ x + y + z ≧ 4.
∵) 3(x + y + z) = 3x + 3y + 3z ≧ 3x + 2y + z ≧ 12.
[数学セミナー編集部編 「数学ガイダンス」 より 「大学数学の心構え」 の中から。]
Tuesday, 3rd December, 2002.
mn + 1 個の実数からなるどのような数列に対しても m + 1 個の数からなる増加部分列か n + 1 個の数からなる減少部分列が存在する。
以下
http://www.cut-the-knot.org/pigeonhole/seq.shtml からの翻訳:
背理法を用いて証明する。 そのような部分列が存在しないとしよう。 与えられた実数列の中の各数 x に対し, x で始まる最長の増加部分列の長さを i, x
で終わる最長の減少部分列の長さを j として, 順序対 (i, j) を作る。 背理法を用いているので 1 ≦ i ≦ m, 1 ≦ j ≦ n
でなければならない。 さて, このようにして, x が mn + 1 個あり, その各々について得られた順序対は高々 mn 種類しかないので,
数列の要素のうち必ず二つこのようにして得られた同じ順序対 (s, t) が対応している。 それらを a, b とし,
与えられた実数列の中でこの順序に出て来るとしよう。
もしも a < b であったとすると, b で始まる最長の増加部分列は (この a を付け加えることによって) 長さが s + 1 となるが, これは a
で始まる最長の増加部分列の長さが s であるということに矛盾している。 だから a ≧ b でなければならない。 しかし一方 a
で終わる最長の減少部分列の長さは, この b を付け加えることによって t + 1 となってしまうが, b で終わる最長の減少部分列の長さが t
であるということに矛盾してしまう。 これ以外に a, b の大小関係はないので, 背理法によって証明された。
区間 [a, b] に於ける cos x の区分求積法による計算。 [数学質問箱,
新掲示板で
aiko 氏の質問への解答]
簡単の為に c = b - a と置く。
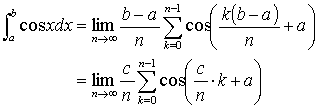
さてここで Euler の公式によって
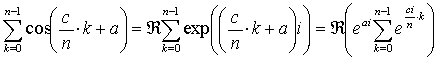
(R は実数部を表す記号). 等比数列の和の公式を用いれば
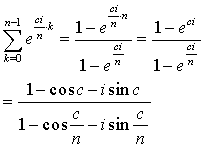
半角の公式 2sin2(θ/2) = 1 - cos θ を (最初分子で, 続いて分母で) 用いると
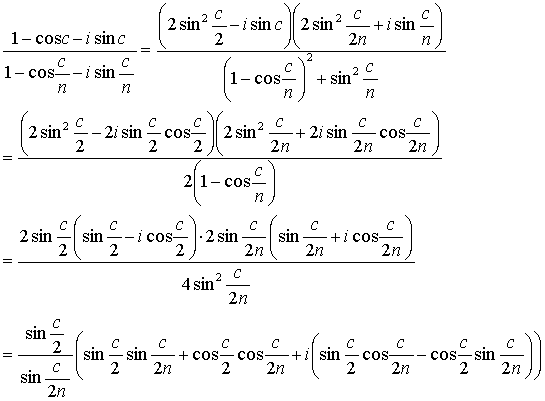
よって
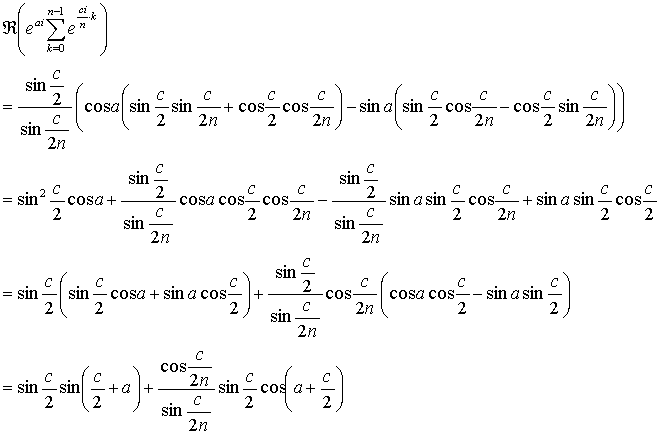
ここで c/2 + a = (b - a)/2 + a = (b + a)/2 であるから
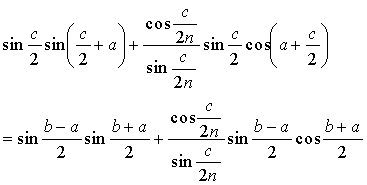
ここで積を和に変える公式を用いると結局
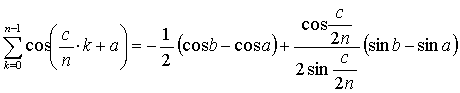
だから [上記も参照のこと]
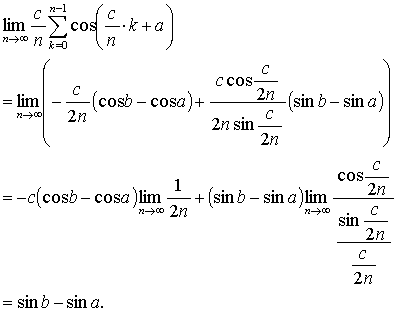
Sn には位相同相だが微分同相でないものが存在する。 通常のものも含めると (向き付けを考えて向きを保つ微分同相写像で分類すると) n = 7 の時 28 種類, n = 8 だと 2
種類, n = 9 だと 8 種類, n = 10 だと 6 種類, n = 11 だと 992 種類。 ところが何故か n = 12 だと 1
種類だけしかない。 [J. W. Milnor, On manifolds homeomorphic to the 7-sphere,
Ann. Math, 64, (1956) pp. 399 -- 405. M. A. Kervaire and J. W. Milnor,
Groups of homotopy spheres: I, Ann. Math, 77 (1963), pp. 504 -- 537.]
(括弧内は 2010/3/2 22:41 の 我疑う故に存在する我 氏のご指摘による。 尚 S7 の場合, 向き付けを考えなければ 15
個だそうである)
p を素数とするとき p-adic number field Qp には Σaipi
→ (Σa2ipi, Σa2i+1pi) という Qp
→ Qp2 の位相同相写像がある。 従って我々の常識に反して Qp
の世界では次元の違いは違いにならない。 R でこういうことが起きないのは 1 = 0.999999... だからだという。
Friday, 29th November, 2002.
p を積分が収束する適当な定数とする。 このとき
∫0π/2 dx/(1 + tanp x) =
π/4.
∫0π/2 dx/(1 + tanp x) = ∫0π/4
dx/(1 + tanp x) + ∫π/4π/2 dx/(1 + tanp
x).
後ろの方で t = π/2 - x と変換すると
与式 = ∫0π/4 dx/(1 + tanp x) + ∫π/40
(-dt)/((1 + tanp (π/2 - t))
= ∫0π/4 dx/(1 + tanp x) + ∫0π/4
dt/( 1 + cotp t)
= ∫0π/4 dx/(1 + tanp x) + ∫0π/4
tanp t dt/(1 + tanp t)
= ∫0π/4 dx = π/4.
2ch BBS の数学板に p = √2 の場合の質問がされていたので。
これは 41st Putnam 1980 の問題だそうである。
The original text and official solutions were published in American Mathematical
Monthly 88 (1981) 607-12. だそうである。
くだらねぇ問題スレ ver.3.1415926535897932384 (3)
S2 の極座標は, S2 の
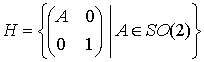 による軌道分解から導かれる。 起点は (sin θ, 0, cos θ) で, これを
による軌道分解から導かれる。 起点は (sin θ, 0, cos θ) で, これを
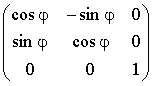 で写したと思えばよろしい。
で写したと思えばよろしい。
松木敏彦
リー群入門 (8)
球函数と SO(3) の作用 (1)
数学セミナー (11), 2002.
R 3 上の Laplacian △ = ∂2/∂x2 +
∂2/∂y2 + ∂2/∂z2 を球面極座標表示に変換するためには,
一度円柱座標 x = ρ cos φ, y = ρ sin φ, z = z に変換してからもう一度, 二次元の極座標変換を用いた方が,
直接球面極座標に変換するよりも易しい。 (工学部では常識だそうだ)
松木敏彦
リー群入門 (8)
球函数と SO(3) の作用 (1)
数学セミナー (11), 2002.
n (≧ 3) 個の球があり, それらの外見は全く同一であるが, 重さについて, 一個だけ例外がある。 天秤を使って重さの比較をする。 自然数 m が 3m
≧ n > 3m-1 を満たすとき, 天秤による比較が m + 1 回以内でその例外球を見つけ,
更にそれが他よりも重かったか軽かったかまでを判定することが出来る [永田雅宜]
n 個の球に, 三進法を用いて 0 から (最大) 3m - 1 までの番号をつける。 形式的に (上の方は 0 を補って) m
桁の数で表す。 即ち 000…00 (= 0), 000…01 (= 1), ......, 222…22 (= 3m - 1)
というように。 このとき次の事実が成り立つ。
つけた番号を全部並べたとき, どの桁についても, 0 の数, 1 の数, 2 の数のうち, 何れか二つは等しいとするような番号の付け方が出来る
(連続していなくて良いが別の球には別の番号を振る)。
[方法 1] n = 3m とするとき, 3r の桁では 0 が 3m-1 個, 1 が
3m-1 個, 2 が 3m-1 個と同数である。
3m > n > 3m-1 では一般にはそうはいかない。そこで最後の番号 (つまり n) に着目する。
ある桁での数字が 0 であれば, その桁では 1, 2 の数は同じであるから良い。 ある桁の数字が 2 であればその桁の 0, 1 の数は同じであるから良い。
問題は 3r の桁の数が 1 である場合である。 この場合, 最後に並ぶ 1 の数を s とする。 その前に続く 0 から最後の s
個を選び, それらの 0 を 1 に替え, 最後の s 個の 1 を 2 に替えると, その桁の 1, 2 の数が同じになる。
念の為に違う番号が振られているかを調べてみると, 替えたところだけを見ると 2s 個の番号に 3r
を加えたことになっているので大丈夫である。
[方法 2] k = 0, 1, 2, ... とする。 最初に 1 から順に番号を割り当てておく。, 3k + 2 番目とは 3k + 1 番目の番号の
0 を 1 に, 1 を 2 に, 2 を 0 に替え, 3k + 3 番目は 3k + 2 番目の番号に同様の操作をする。 この操作では球の数が 3
の倍数ならば明らかに要請を満たしている。 そうでない場合は最後の 1 又は 2 個だけが例外だから大丈夫である。
さて, 上記のように番号付けした上で, 次の操作を行う。 各桁毎にその桁の数字のうち, 数の等しい二組を選ぶ。 それらを番号に持つ球を天秤の両側に載せる。
(1) それらの重さが異なるときは重かった組の数字をその桁の x の数字とし, 軽かった組の数字を y の数字とする。
(2) 等しかったときには, 載せなかった球の番号の数字を x, y のその桁の数字とする。
この操作は全部で m 回で, それによって番号 x, y が決まる。
例外球がその他のものよりも重い場合, その番号は x でなければならない。 同様に軽い場合は y でなければならない。 そこで番号が x, y 以外の球
(それは例外ではない) と番号 y の球を天秤で比較する。 重さが違えば, 番号 y が軽い例外球であり, 同じであれば番号 x が重い例外球である。
[別法]
先ず n = 2a + c, (a ≦ 3m-1, c ≦ 3m-1) として n 個の球を二つの a 個の集団
A, B と c 個の集団 C とに分け, A, B を天秤に載せて比較する (以下帰納法)。 同じ重さであれば例外球は C の中にあり, この場合帰納法により
C からは m 回で判定できるので結局 m + 1 回で判定できることになる。 重さが異なる場合, 軽かった方の集団を A と名付け直す。
(1) a が偶数のときは, A を二等分して, A1, A2 とし, これらを比較する。 これらが釣り合う場合は
B に例外球がある。 釣り合わなければ A1, A2 の何れか軽い方に軽い例外球があるので,
何れにしても帰納法により終了。
(2) a が奇数の場合は, A に 例外ではない球 (例えば C) から球を一つ加えて同様に比較する。
[他にもあるが省略]
エレガントな解答をもとむ
[解答]
数学セミナー (11), 2002.
Sunday, 24th November, 2002.
球面に内接する四面体 O-ABC で a = OA, b = OB, c = OC とするとその外心 P の位置ベクトルは
OP = (a2OB×OC
+ b2OC×OA + c2OA×OB)/(OA・(OB×OC))
である (太字イタリックは vectors)。
Friday, 15th November, 2002.
n ∈ N が奇数の時
Πk=1n-1 tan(kπ/n) = (-1)(n-1)/2n.
塚本 (?)
【徹底】ネット数学者総合スレ III 【検証】
388 (16:58 31st Oct 2002)
1998 年の column の冒頭に載っているように sin nθ = 2n-1
Πk=0n-1 sin (θ + kπ/n) である。 ここで θ = x + π/2 を代入すると sin n(x
+ π/2) = 2n-1
Πk=0n-1 sin (x + kπ/n + π/2).
加法公式によって (便宜的に n = 2m + 1 とする)
sin n(x + π/2) = sin(nx + mπ + π/2) = cos(nx + mπ) = cos nx cos mπ = (-1)m
cos nx = (-1)(n-1)/2 cos nx.
sin (x + kπ/n + π/2) = cos(x + kπ/n).
従って (-1)(n-1)/2 cos nx = 2n-1
Πk=0n-1 cos(x + kπ/n) である。 これと元の式 sin nx = 2n-1
Πk=0n-1 sin (x + kπ/n) とから辺々割算して
Πk=0n-1 tan (x + kπ/n) = (-1)(n-1)/2 tan nx.
従って
Πk=1n-1 tan (x + kπ/n) = (-1)(n-1)/2 (tan nx)/tan
x.
ここで x → 0 とすれば
lhs = Πk=1n-1 tan (kπ/n)
rhs = (-1)(n-1)/2 limx→0 ((sin nx)/(sin x)・(cos x)/(cos nx))
= (-1)(n-1)/2 limx→0 (n (sin nx)/(nx)・x/sin x) = (-1)(n-1)/2n.□
Sunday, 3rd November, 2002.
ζ(2) = Σn=1∞ 1/n2 = π2/6 の初等的な証明
黒川重信
数学セミナー (10), 2002.
最高次の係数の符号が (-1)n-1 である n - 1 次多項式 Pn(x) と, 最高次の係数の符号が
(-1)n である n 次多項式 Qn(x) が存在して, 全ての実数 θ に対して
sin(2nθ) = n sin(2θ)Pn(sin2θ),
cos(2nθ) = Qn(sin2θ)
を満たす。
東京工業大学後期日程 (12th March, 1990)
旺文社大学入試問題正解
数学 国公立大編 90 による
[証明]
sin 4θ = 2 sin 2θ cos 2θ = 2 sin 2θ (1 - 2sin2θ),
cos 4θ = 2 cos22θ - 1 = 2(1 - 2sin2θ)2 - 1 = 8
sin4θ - 8sin2θ + 1
であるから, P2(x) = 1 - 2x, Q2(x) = 8x2 - 8x - 1
として成立する。
n で成立するとして n + 1 での成立を言おう。
sin 2(n + 1)θ = sin(2nθ + 2θ)
= sin 2nθ cos 2θ + cos 2nθ sin 2θ
= n sin 2θ Pn(sin2θ)(1 - 2sin2θ) + Qn(sin2θ)sin
2θ
= sin 2θ (nPn(sin2θ)(1 - 2sin2θ) + Qn(sin2θ))
= (n + 1)sin 2θ・(nPn(sin2θ)(1 - 2sin2θ) + Qn(sin2θ))/(n
+ 1).
cos 2(n + 1)θ = cos(2nθ + 2θ)
= cos 2nθ cos 2θ - sin 2nθ sin 2θ
= Qn(sin2θ)(1 - 2sin2θ) - n sin2 2θ
Pn(sin2θ)
= Qn(sin2θ)(1 - 2sin2θ) - 4n sin2 θ
(1 - sin2θ)Pn(sin2θ).
今
Pn(x) = (-1)n-1pn xn-1 + …,
Qn(x) = (-1)n qnxn + …,
pn-1, qn > 0,
Pn+1(x) = (nPn(x)(1 - 2x) + Qn(x))/(n + 1),
Qn+1(x) = Qn(x)(1 - 2x) - 4nx(1 - x)Pn(x)
と置くと
Pn+1(x) = (-1)n(2npn + qn)xn/(n
+ 1) + …,
Qn+1(x) = (-1)n+1(2qn + 4npn)xn+1
+ …□
上記の Pn(x) で Pn(x) = Πk=1n-1 (1 -
x/sin2 (kπ/(2n))).
東京工業大学後期日程 (12th March, 1990)
旺文社大学入試問題正解
数学 国公立大編 90 による
[証明]
0 < θ < π/2 とすると sin 2θ > 0 である。 又
Pn(sin2θ) = (sin 2nθ)/(n sin 2θ)
従って
limθ→0 Pn(sin2θ) = limθ→0 ((sin
2nθ)/(2nθ)・(2θ)/sin 2θ) = 1.
だから Pn(0) = 1 である。 よって Pn(x) の定数項は 1.
更に Pn(sin2θ) = 0 と置くと sin 2nθ = 0 であって 0 < 2nθ < nπ
であるから 2nθ = kπ, 1 ≦ k ≦ n - 1 である。 つまり Pn(x) の零点は n - 1 個あり, x = sin2θ
= sin2(kπ/(2n)), 1 ≦ k ≦ n - 1 である。 0 < θ = kπ/(2n) < π/2 より,
これらは全て異なる。あとは Pn(x) が n - 1 次であり, 最高次の係数が (-1)n-1 であること,
定数項が 1 であることから証明される。□
さて以上の二つから
sin(2nθ) = n sin(2θ)Πk=1n-1 (1 - ((sin θ)/sin(kπ/(2n)))2)
が分かる。 ここで θ = x/(2n) に置き換えて
sin x = n sin(x/n) Πk=1n-1 (1 - ((sin
(x/(2n)))/sin(kπ/(2n)))2)
で n sin(x/n) = x・sin(x/n)/(x/n),
(sin (x/(2n)))/sin(kπ/(2n))
= (x/(kπ))・sin (x/(2n))/(x/(2n))・(kπ/(2n))/sin(kπ/(2n))
であることを用いて n → ∞ とすると
sin x = x Πk=1∞ (1 - x2/(k2π2))
が得られる [L. Euler の方法]。
これと sin x の Taylor 展開の x3 の項の係数とを比較して, Euler は ζ(2) = Σn=1∞
1/n2 = π2/6 を出したのだという。
しかし次の方法によっても出る。 先ず
Σk=1n-1 1/sin2(kπ/(2n)) = 2(n2
- 1)/3.
東京工業大学後期日程 (12th March, 1990)
旺文社大学入試問題正解
数学 国公立大編 90 による
[証明] (上記の Pn(x) と Qn(x) を使う。)
先ず Pn(0) = Qn(0) = 1 である。 そこで Pn(x) = 1 - anx
+ …, Qn(x) = 1 - bnx + … と置く。 すると上記の結果から
Pn+1(x) = (nPn(x)(1 - 2x) + Qn(x))/(n + 1)
= (n(1 - anx + …)(1 - 2x) + (1 - bnx + …))/(n+1),
Qn+1(x) = Qn(x)(1 - 2x) - 4nx(1 - x)Pn(x)
= (1 - bnx + …)(1 - 2x) - 4nx(1 - x)(1 - anx + …)
であるから
an+1 = (n(an + 2) + bn)/(n + 1) … (a),
bn+1 = bn + 2 + 4n … (b).
(b) より n ≧ 3 に於て
bn+1 = b2 + Σk=2n-1(2 + 4k) = 8 + Σk=2n-1(2
+ 4k)
= Σk=0n-1(2 + 4k) = n(2 + 2 + 4(n - 1))/2
= n(1 + 1 + 2(n - 1)) = 2n2
(これは n = 2 の場合をも含んでいる).
Pn(x) = Πk=1n-1 (1 - x/sin2 (kπ/(2n)))
の x の一次の係数を比較すると
an = Σk=1n-1 1/sin2(kπ/(2n)), a2
= 2
が分かる。 an = 2(n2 - 1)/3 を証明すればよい。 n = 2 の時は成立している。n
で成立しているとして n + 1 での成立を言おう。 上記の (a) より
an+1 = (n(an + 2) + bn)/(n + 1)
= (n(2(n2 - 1)/3 + 2) + 2n2)/(n + 1)
= n(2n2 - 2 + 6 + 6n)/(3(n + 1))
= n(2n2 + 6n + 4)/(3(n + 1))
= 2n(n + 1)(n + 2)/(3(n + 1))
= 2n(n + 2)/3
= 2(n2 + 2n)/3
= 2((n + 1)2 - 1)/3□
(別証) an = Σk=1n-1 1/sin2(kπ/(2n))
と置く。 Pn(x) = 1 - anx + cnx2 + …
と書ける。 x ≠ 0 の時
(Pn(x) - 1)/x = - an + cnx + ….
即ち an = -limx→0 (Pn(x) - 1)/x. 従って
an = -limθ→0 (Pn(sin2θ) -
1)/sin2θ = -limθ→0 (sin 2nθ - nsin 2θ)/(n sin 2θ sin2θ).
Taylor の定理から sin x = x - x3/6 + o(x3) を用いて代入しても求められる (略)。
さて 0 < θ < π/2 ⇒ sin θ < θ < tan θ だから
1/sin2θ > (1/θ)2 > (1/tan θ)2 = (1/sin θ)2
- 1.
この式で θ = kπ/(2n), k = 1, 2, ..., n - 1 としたものを辺々加え, 先程証明した
Σk=1n-1 1/sin2(kπ/(2n)) = 2(n2 -
1)/3
を用いると
2(n2 - 1)/3 > (4n2/π2)Σk=1n-11/k2
> 2(n2 - 1)/3 - (n - 1)
つまり (π2/6)(1 - 3/(2n) + 1/(2n2)) < Σk=1n-11/k2
< (π2/6)(1 - 1/n2) となって n → ∞ とすると, 目標の ζ(2) = Σn=1∞ 1/n2 = π2/6
が言える。
Tuesday, 15th October, 2002.
x > 0 で 1 ≦ m < n を自然数とする。 このとき
((m + x)/n)n ≧ (x/(x - m))n-m
が成り立つ。 これは相加平均相乗平均の関係を用いて
lhs = (((m 個の 1) + (n - m 個の x/(x -m)))/n)n
≧ (n√(1m・(x/(x - m))n - m))n = rhs
と証明できる。
大島邦夫
エレガントな解答を求む
数学セミナー (8), 2002.
1657 年,フェルマーは
x2 - 61y2 = 1,
x2 - 109y2 = 1
を満たす解を見つけよという挑戦状を他の数学者に送った。 これを解いたのはウォリスとブラウンカーで, ウォリスは 「ブラウンカーの方法」 として,
本質的に連分数を用いる解の発見法を発表するが, 不幸なことに後に L. Euler が 「ペルが解法を発見した」 と間違えたために, x2
- ny2 = 1 の自然数解を求めるという問題がペル方程式と呼ばれるようになったそうである。
木村俊一
電卓で数の正体を見破ろう
数学セミナー (9), 2002.
ENIAC = Electric Numerical Integrator And Calculator.
私は programming こそが 「新しい数学」 だと思っています。Programming 固有の命令や概念を使いこなすこと,
これはまさに数学なのです !
堀内明
実数係数の一変数多項式 p(x) が全ての実数 x について p(x) > 0 を満たすならば p(x) は最小値を持つ。しかし, 二変数多項式 p(x,
y) につい てはこれは正しくない。例: p(x, y) = (xy - 1)2 + y2.
一変数多項式 h(x) が無限に多くの有理数 r について h(r) が有理数になるならば h(x) の係数は全て有理数である (実は n = deg h
とするとき相異なる n + 1 個の有理数に対し h(x) が有理数値になるならば有理係数多項式であることが, 次数 n に対する数学的帰納法で示される)。
更に既約な分数式 h(x) = f(x)/g(x) についても同じことがいえる (詳しくは m = deg f, n = deg g とするとき, 相異なる m
+ n + 1 個の有理数に対し h(x) が有理数値になるならば, h(x) が有理係数であることが, m + n に関する数学的帰納法で示される)。
米澤佳己
エレガントな解答を求む
数学セミナー (9), 2002.
竹井力, 微積分は面白い --- 円と球の求積法 ---, 現代数学社
これには球の体積, 表面積の公式の証明が 13 通りも述べられているそうである。
[ランバートの公式]
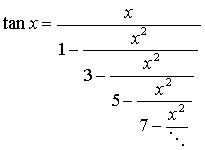
物理のブラベクトルとケットベクトル (Dirac 流) について。
vj が vector, vj をその双対としよう。
<j| = vj をブラベクトル bra-vector,
|j> = vj を ket-vector という。
<j|k> = δjk は内積。|k><j| は行列単位 (vk と
vj のtensor product).
<k|f|j> = <k| f(vj)> = fkj. これから f = Σk,j
|k>fkj<j| = Σk,j |k><k|f|j><j|.
1 = Σj |j><j| (1 の分解), f が対角化可能な線型変換で vj が
eigenvalue λj の eigenvector だとすると f = Σj |j>λj<j|.
Pj = |j><j| が vj 成分への射影であり (Pjv
= PjΣk |k>xk = |j><j|Σk |k>xk
= |j>xk であり PjPk = |j><j|k><k| = |j>δjk<k|
= Pjδjk.
90° = 100g = 8 points = π/2. 記号 g は grade,
pointは航空や航海の分野で用いられるものである。
Wednesday, 18th September, 2002.
公式 [仁平政一, 茨城県立藤代高等学校]
p ∈ Z+ ⇒
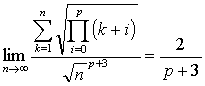
証明は先ず √kp+1 < √Πi= 0n(k + i) < √(k + p)p+1
から, Σk=1n √kp+1 > ∫0n √xp+1
dx を区分求積法で言い, 同様に Σk=1n-1 √(k + p)p+1 > ∫0n
√(x + p)p+1 dx を言ってから挟み撃ちする。
数研通信, 数学 No. 44.
数研出版
対数の底の変換公式の裏技 [塩見浩三, 愛媛県済美平成校]
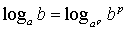 .
.
(original は p = 2) これを見ていて思いついたのが公式
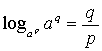 (証明は共に底の変換公式を用いれば直ぐにできる)。
(証明は共に底の変換公式を用いれば直ぐにできる)。
数研通信, 数学 No. 44.
数研出版
内角の一つが α である平行四辺形が, x, y 平面の楕円 x2/a2 + y2/b2
= 1, 0 < b < a に 4 点で外接しているとする。 このうちの, 隣り合う二辺上の接点を P1(a cos θ1,
b sin θ1), P2(a cos θ2, b sin θ2)
とするとき, その平行四辺形の面積は 4ab/sin|θ1 - θ2|.
[キャンベル-ハウスドルフの公式]
A, B: 行列, [A, B] は Lie bracket として
exp(tA)exp(tB) = exp(t(A + B) + (t2/2)[A, B] + (t3/3)([A,
[A, B]] + [[A, B], B])/2 + …)
Tuesday, 17 September.
公式 [平面三角太郎 Thursday, 18th July, 2002.]
sin2α - sin2β = sin(α + β)sin(α - β)
証明:
rhs = (sin α cos β + cos α sin β)(sin α cos β - cos α sin β)
= sin2α cos2β - cos2α sin2β
= sin2α(1 - sin2β) - (1 - sin2α)sin2β
= sin2α - sin2α sin2β - sin2β + sin2α
sin2β = lhs□
最初この式を見たとき, 初学者のよくやる間違いかと思ってしまった (^_^;
Toshio Sekiya
氏が次のような別証明をしてくれた。
rhs = (sin α - cos β)(sin α + cos β)
= 2sin((α + β)/2)cos((α - β)/2)・2cos((α + β)/2)sin((α - β)/2)
= (2sin((α + β)/2)cos((α + β)/2))(2sin((α - β)/2)cos((α - β)/2))
= lhs.
角度の単位に pt (point = 点) というのがある。
1 pt = 11.25゜= 360゜/32 で, これは航海や航空分野で用いるのだそうだ。
[トロッターの公式]
limh→0 (h log(ea/h + eb/h)) = max(a, b),
limh→0 (h log(ea/h × eb/h)) = a + b.
Monday, 13th May.
Σk=1n (k!k) = (n + 1)! - 1.
(証明は数学的帰納法で)
Sunday, 5th May.
Waring (ウォーリング) の問題 (1770)
n, N を自然数 (正の整数) とする (以下固定する)。
任意の自然数 A を自然数 xi , i = 1, 2, ... , N
を用いて
A = x1n + x2n + … +xNn
と表せ, n を固定したとき, 全ての A
をこのように表示できるような, 最小の N = N(n) を求めよ。
Lagrange (1770): N(2) = 4.
Wieferich (ヴィーフェリッヒ) (1912): N(3) = 9.
Chen (チェン) (1964): N(5) = 37.
それ以外についてはまだ知られていない。
Friday, 19th April.
Digital 信号処理の分野で取り扱う analogue 信号は全て,
超函数の Fourier 変換になっている。
数学ではこの事実をペーリー-ウィーナーの定理と呼ぶ。
吉野邦生
ディジタル信号と母函数
数学セミナー (10), 2001.
[2001 年の column に載っている, 仁平政一の公式の拡張]
函数 f(x) は非負, 即ち f(x) ≧ 0 で, x ≧ 0
で連続且つ単調増加とする。 函数 f(x) の原始函数の一つを
F(x) 年, q は 0 < q ≦ 1 であるような定数とする。このとき,
次の二つが成り立つ。
(1) 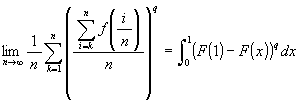 ,
,
(2) 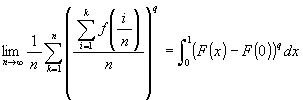 .
.
熊野充博, 数学セミナー (3), 2002.
[証明] (1) も (2) も同様なので, (1) のみ示す。
簡単のために, 右辺の q 乗されている括弧の中を Sn
と置く (つまり左辺は limn→∞(1/n)Σk=1nSnq)。
このとき, graph を見れば ∫(k-1)/n1 f(x)dx ≦ Sk
≦ ∫k/n1 f(x)dx + f(1)/n が分かる。 ここで
∫(k-1)/n1 f(x)dx = F(1) - F((k-1)/n),
∫k/n1 f(x)dx = F(1) - F(k/n)
であり, F'(x) = f(x) ≧ 0 より F(k/n) ≧ F((k-1)/n) であるから
F(1) - F(k/n) ≦ Sk ≦ F(1) - F(k/n) +
f(1)/n.
これを q 乗すると (a ≧ 0, b ≧ 0 の時 (a + b)q ≦ aq
+ bq より)
(F(1) - F(k/n))q ≦ (Sk)q ≦ (F(1) - F(k/n)
+ f(1)/n)q ≦ (F(1) - F(k/n))q + (f(1)/n)q.
従って
(1/n)Σk=1n (F(1) - F(k/n))q ≦ (1/n)Σk=1n
(Sk)q ≦ (1/n)Σk=1n (F(1) - F(k/n))q +
(f(1)/n)q.
よって n→∞ で所謂区分求積法 (Riemann 積分) を用いると,
「挟み撃ちの原理」 から証明される。□
前へ
次へ
コラムの墓場の目次へ
HOME
![]() .
.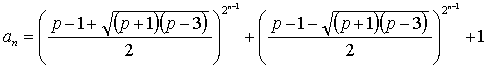
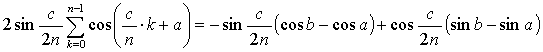
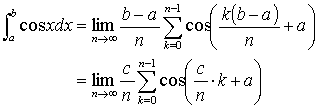
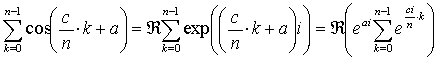
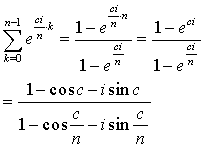
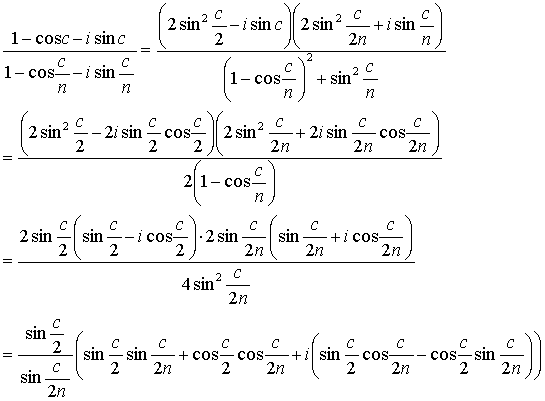
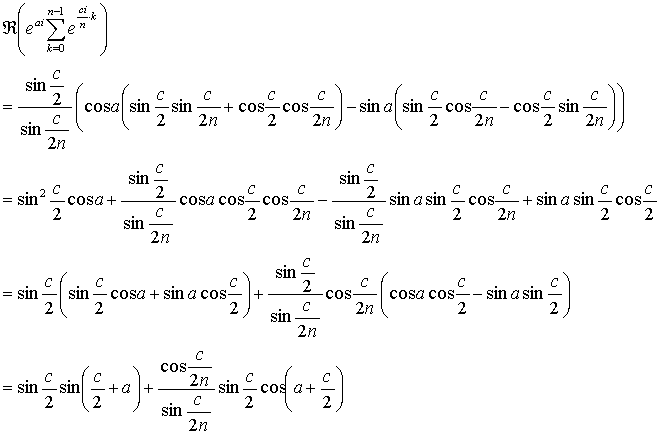
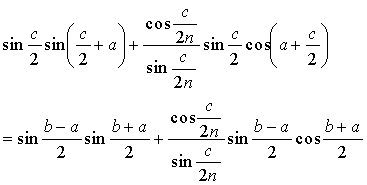
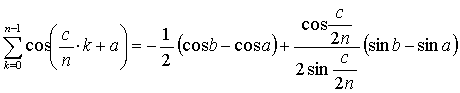
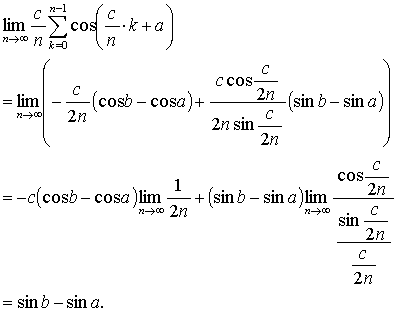
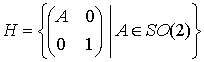 による軌道分解から導かれる。 起点は (sin θ, 0, cos θ) で, これを
による軌道分解から導かれる。 起点は (sin θ, 0, cos θ) で, これを
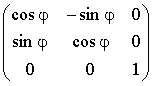 で写したと思えばよろしい。
で写したと思えばよろしい。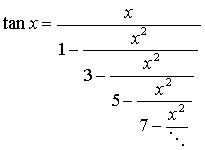
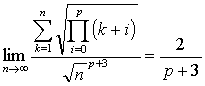
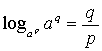 (証明は共に底の変換公式を用いれば直ぐにできる)。
(証明は共に底の変換公式を用いれば直ぐにできる)。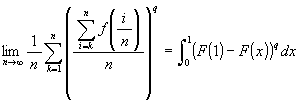 ,
,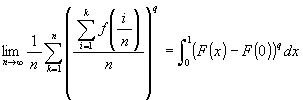 .
.