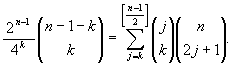
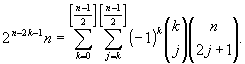
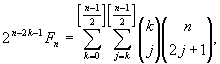 Fnはフィボナッチ数.
Fnはフィボナッチ数.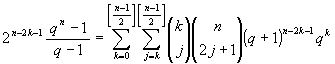
Nature and nature's laws lay hid in night.
God said, Let Newton be and all was light.
Alexander Pope
21st May 1688-30th May 1744.
(自然と自然の諸法則は夜に隠されていた
神は言われた「ニュートンあれ」とそして光があった
アレグザンダー・ポープ)
μὴ ει’ˆναι βασιλικὴν α’ τραπὸν ε’πὶ γεωμετρίαν. (幾何学に王道なし)
ユークリッド
μηδεὶς α’γεωμέτρητος ει’σίτω. (幾何学を知らざるもの入るべからず)
プラトン
‛όπερ ’έδει δειˆξαι (quod erat demonstrandum 証明終わり)
極小曲面と呼ばれる曲面がある。 空間内に与えられた閉曲線 C に対し, C を境界とする極小曲面の存在は T. ラドー (1930) と J. ダグラス (1931) による。 Geometry Analysis Numerics Graphics (GANG) に幾つかの曲面の図画がでている。 Costa-Hoffman-Meeks の極小曲面 (1982) や, 1984 年に H. Wente が球面以外に平均曲率一定の閉じた曲面の存在を示したが, その画像 などが面白い。 カポレアスは任意数個の穴のあいた閉じた平均曲率一定の曲面の存在を示している。
△ABC の内接円が三辺 BC, CA, AB と接する点を X, Y, Z とすると,
三直線 AX, BY, CZ は一点に会する。 この点をジェルゴンヌ点 (Gergonne)
という。 傍接円についても同様。
△ABC の外心 O に対する垂心 H の対称点を
ド・ロンシャン点 (G.
de Longchamps) という。
内心 I, ジェルゴンヌ点 G, ド・ロンシャン点 L
は同一直線上にある。 傍心についても同様。
ド・ロンシャン点は次の性質も満たしている:
(1) Euler 線上に垂心, 重心, 外心, ド・ロンシャン点の順に 2 :
1 : 3 の比に並んで調和点列を成す。
(2) △ABC
を各辺の中点に対して対称変換すると結果として大きな一つの三角形ができる。
この三角形に対し元の三角形は中点三角形であるが,
ド・ロンシャン点はこの大きな三角形の垂心になっている。
[Michael Loguet-Higgins, A Fourfold Point of Concurrence Lying on the Euler
Line of a Triangle, The Mathematical Intelligencer, Springer-Verlag, vol. 24,
no. 1, (2000), pp. 54-59.]
問題: ここに 12 個の coins があって, 一つだけ偽金が混じっていることが分かっている。 この偽金は本物と重さが違うことだけが分かっていて, 重いか軽いかについては不明である。 この偽金を天秤を三回だけ使ってどれがそうであるかと本物より重いのか軽いのかを判定せよ。
答:
先ず coins に a, b, c, d, e, f, g, h, i, j, k, l と名前を付ける。
最初に a, b, c, dとe, f, g, h を天秤にかけよう。
どちらが重いかによって三つの場合がある。
1. それらが等しい場合。
ここで i, j と a, k とを比較しよう。
1.1 それらが等しい場合。
この場合偽物はlと確定しているので, a と比較すれば偽物lは本物より重いか軽いかが確定する。
1.2 i, j の方が重い場合。
この場合は i, j, k のどれかが偽物である。そこで i と j を比較する。
1.2.1 i と j が等しい場合。
偽物は k である。しかも k がはいった方が重いのだから, k は重い。
1.2.2 i の方が重い場合。
偽物は i か j であるが, この場合 i と j の合計が本物二つよりも重いのだから,
i は重い。
1.2.3 i の方が軽い場合。
上記と同様にして, j が偽物で本物よりも重い。
1.3 i, j の方が軽い場合
1.2 の場合と同様で, 軽重が逆転するだけである。
2. a, b, c, d の方が重い場合
この段階で i, j, k, l は本物と確定する。そこで, a, b, g と c, d, h
を比較する。
2.1 それらが等しい場合。
この場合除かれている e, f のどちらかが偽物である。
これらがはいっている方が軽いのだから,
偽物はこれらを天秤にかけて軽い方である。
2.2 a, b, g の方が重い場合。
とりあえず a, b を比較する。
これらのうちどちらか重い方があったとすれば,
それが偽者であると確定する。
そうでない場合にはこの比較では g が偽物で重いか,
c, d, h のいずれかに偽物で軽いものがあると結論されるが,
もともと a, b, c, d よりも e, f, g, h の方が軽いのだから, g
が偽物で重いということはありえない。 従って,
c, d, h のいずれかが軽い偽物である。 しかし a, b, c, d は e, f, g,
h より重いのだから, c 又は d が軽いということはありえないので,
h が軽い偽物と確定する。
2.3 a, b, g の方が軽い場合。
2.2 と同様にして, c, d を比較し,
どちらか重いものがあればそれが偽物。
そうでなければ同様の推論により g が軽い偽物と確定する。
3. a, b, c, d の方が軽い場合。
2 と同様である。 推論を除いて判定だけ書く。 先ず a, b, g と
c, d, h を比較する。
3.1 それらが等しい場合。
この場合 e と f と比較して重い方が偽物。
3.2 a, b, g の方が重い場合。
先ず c と d とを比較して軽い方が偽物, 等しければ g が重い偽物。
3.3 a, b, g の方が軽い場合。
先ず a と b を比較して軽い方が偽物, 等しければhが重い偽物。
[一般的には 「偽コインの問題」 を参照せよ]
普通使われている Euclidian metric は,
基本的に格子点どうしの距離しか扱わない digital
画像処理にはあまり適さない。 それは,
距離が無理数になってしまう可能性があるからである。
これより少しましなのが,
この近似であり, 結果が高々有理数になる octagonal metric で,
これは, 原点と点 P(x, y) との距離を
max(|x|, |y|, 2|x + y|/3)
で定義するものである。 最も良く使われるのは, city block
metric (市街地距離, Manhattan metric) |x| + |y| と chess board metric
max(|x|, |y|)
である。明らかにこれらは格子点の場合有理整数値になるので都合がよいのである。
数学は若者の game ではなく, 若くなければ出来ないという考えは誤っている。 数学者は, 自らを数学者たるべく長い年月に渉って自己を鍛練すべきである。 そして頂点に達した水準を長く保つよう努めるのが望ましい。
志村五郎
数学者連環記, 1982
未来の数世紀を通じての, 我々の科学に差し迫っている進歩とその発展の秘密とを, 一目見ようとして, その下に未来が隠されている veil を進んで取り除こうとしない者が, 我々の中に誰かいるだろうか ! 未来の人々の指導的な数学的精神が追及しようとしている特別な目標は何であろうか ? 新しい世紀が数学的思考の拡大で豊富な野に, どのような新しい方法と新しい真理を見出すであろうか ?
Hilbert
数学の問題, 共立出版, 1969
一松信訳
予想:
n を n ≡5, 6, 7 (mod 8)
を満たす平方因子を持たない正の整数とするとき, n
を面積として持つ三辺が有理数の直角三角形が存在する。
(See
N. Koblitz Introduction to elliptic curves and modular forms, GTM 97, Springer-Verlag.)
数学の難問に賞金がかかることの背景には,
二十一世紀の科学の発展に対する危惧があるのではないかと思っています。
最近の若者を見ていると,
どうも, お金儲けに関心が向いている人が多く,
じっくりと科学の研究に取り組もうという意欲が弱いように感じられます。
必死に頑張った人に成長してから "ゆとり"
が出てくるのではないでしょうか。
西野哲朗
理論計算機科学
有名なビュッフォン針の実験というのがあって,
良くご存知であると思われるが, これは間隔が d の平行線が無限に沢山並んでいる所へ長さ
l
(< d) の針を投げて, 平行線と交わる確率が 2l/πd になるというのがそれである
(1770)。
1850 年にウォルフが l/d = 0.8 で 5000 回投げ, 2532 回当たったと報告し,
円周率はこの場合計算上約 3.15955… である。
ラッツェリニという人は 1901 年に l/d
= 0.83, 3408 回投げて 1808 回当たったとの報告をしこのときの円周率は計算上
3.1415929 を得たとしているが
L. Barge rは Lazzerini's Lucky Approximation of π, Math. Mag. 67 (1994), 83-91で疑問を提出している。
生物学の具体的な描写に見られる卑俗さと, 人文科学に見られるかなり漠然とした知的遊戯との中間点を, 数学が供給できる。
ルネ・トム (弥永康夫訳)
自然科学に於ける質的なものと量的なもの
科学 (5), 1978.
科学において知的である権利を持つのは数学者だけである。 [何故なら] 数学者は自らの叡智を証明の後ろに隠すことを知っているからである。
ルネ・トム
(弥永康夫訳)
自然科学に於ける質的なものと量的なもの
科学 (5), 1978.
の部分からの要約。
高次元圏論が明るみに出すこと --- 数学には解消できない不定性が根底にあるということ --- は <内部観測を捨象しない数理> へ自然に繋がっていると思われる。
自然数 n に関し, a1 + a2 + … + an > 0 を満たす
n 個の実数があるとき,
その中から k 個を選んで作る nCk 個の和のうち,
正である和の最小値を p(n, k) と書くことにする。
定理 [Singhi]
p(n, k) = n−1Ck−1.
定理
n = 3, 5 ⇒ p(n, 2) = n - 2,
n ≠ 3, 5 ⇒ p(n, 2) = n - 1.
更にn > 10kkのとき
定理 [Shinghi and Manikam]
n ≧ 3k ならば p(n, k) = n−1Ck−1.
(n > 10kkとは限らない場合については open question)
マルサスは時刻 t に於ける人口を N(t), 増殖率を α とするとき dN(t)/dt =αN(t) とした。
CD 等の digital 録音の原理に, 音の上限の周波数の二倍の sampling 周波数を使えばその上限まで完全に復元できるという Shanon の標本化定理が用いられている。 (これは Whittaker も気づいていたということである。 Whittaker-Shanon-染谷の sampling 定理という)
1980 年代に, ベクトル空間の基底の存在を仮定すると選択公理が導けることが証明されている。
明治大学理工学部数学科阿原研究室のHP
E. H. Weber (1795-1878) と Gustav T. Fechner (1801-1887) による聴覚の法則により常用対数を用いて dB という単位が設定された。
数論は実験科学だ。
J. テイト
世間で私をどう見ているか知りませんが, 私自身としては, 波打ち際で戯れている子供に過ぎないと思っています。 眼前には, 真理の大洋が研究されないまま無限に広がっているというのに, 普通よりは色の綺麗な小石や貝殻を見つけて喜んでいる子供に過ぎないと思っています。
ニュートン
100c + y 年 m 月 d 日の曜日が
[21c/4] + [5y/4] + [26(m + 1)/10] + d‐1 (mod 7)
(0 が日曜) となるというのは 1887
にゼラー (Zeller) が考えたということだ。
藤村幸三郎, 田村三郎: 数学歴史パズル
---数学者も頭をひねった 75 問
講談社ブルーバックス, B592, 1985.
12 さんすう 34 数学 5 Go! にここが link されていて Zeller の読みが, ゼラーかツェラーかというようなことが書いてあるが, ゼラーは英語読み, ツェラーはドイツ語読みである。 Zeller 本人がどういう言語系統の人か分からないが, どちらでも良い。 例えば Dirichlet は本来フランス系の人なので 「ディリショレ」 と読むべきだそうだが通常ディリクレと読まれているようなものである。 (Friday, 20th March 2004.)
(数学の研究で) 正しいことと意味のあることは違う。
山口昌哉
単記投票方式は社会的決定理論家の間では不合理性の明らかなものとして排斥されている。
佐伯胖
きめ方の論理
東京大学出版会, 1980.
アロー (K. J. Arrow) の一般可能性定理 (general possibility
theorem)
二人以上で三つ以上の選択肢を好ましい順に並べる合理的な決め方は,
誰かが独裁者になるしかない。
K. J. Arrow, Social Choice and Individual Values, 2nd ed., John Wiley and Sons,
1963.
初項が a0 である数列 {an} の第 k 階階差数列が定数 αk となっている場合に, 第 l 階階差数列の初項を αl と置くと n ≧ k のとき an = Σl=0k nClαl.
[宗永展卓, 16歳 (当時), NOTE, 数学セミナー (2), 2001]
公式
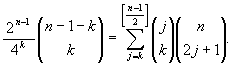
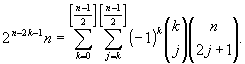
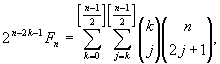 Fnはフィボナッチ数.
Fnはフィボナッチ数.
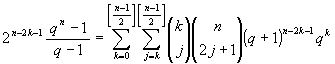
[桑野耕一, 数学工房, 数学セミナー, (2), 2001.]
数学的アイデアの理解とそれが我々の身体と脳からいかにして生まれるかを理解することによって, 脳の数学こそが数学であり, それこそが我々が知り, 又知ることの出来る唯一つの数学なのだということが分かるだろう。
ジョージ・ラコフ (言語学者), ラファエル・ヌニェス (心理学者)
Where Mathematics comes from. (2000 年発刊)
Einstein は, 数学を必要に応じて学べば良いものと考えていたそうであるが, 一般相対性理論を進めるのに Gauss の曲面論を発展させた tensor 解析が必要になって, 数学を大いに学ばなければならないことを痛感させられた。 ある本によれば, 数学者 Hilbert は 「物理学は物理学者に任せておけない段階に入ってきた」 と言ったそうである。
(ある特異積分を含む非線型微積分方程式のセミナー上で
「その被積分函数がどういう条件を満たせば,
それは方程式として意味を持つのか」 という質問に対して)
そういう条件などどうでもいい。
それでどういう解が出てくるのか,
それが面白かったら,
条件なんて幾らでも拡張したらいいじゃないか。
佐藤幹夫
数学は実験である。
Leonhard Euler
Euler にかえれ。
佐藤幹夫
n 次元単位球の表面積 S(n−1)
のちょっと面白い計算方法を紹介します。 ![]() という関数を、R n で二通りの方法で計算します。
という関数を、R n で二通りの方法で計算します。
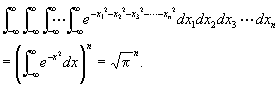
さて一方, 同じ積分を極座標で計算すると, ![]() となりますが,
t = r2 とおけば, これは
となりますが,
t = r2 とおけば, これは ![]() となります。 ここで Γ はガンマ函数です。
両者の積分結果は等しいはずですから
となります。 ここで Γ はガンマ函数です。
両者の積分結果は等しいはずですから 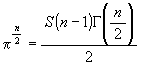 ,
即ち
,
即ち 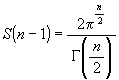 が得られます。
これに rn−1 を掛けて, r で 0 から 1 まで積分すれば,
n 次元単位球の体積
が得られます。
これに rn−1 を掛けて, r で 0 から 1 まで積分すれば,
n 次元単位球の体積 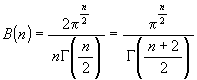 が得られます。
が得られます。
数学は story として語るべきである。 教科書は, 計算の手引書ではなく, 同じ教科書を使っていても, 先生によって語られる内容は違ってくる。
岩井齊良
И. П. Натансон (ナタンソン) による ![]() の証明 (Краткий
Курс Высшей Математики 高等数学の簡単な教程, 1963)
の証明 (Краткий
Курс Высшей Математики 高等数学の簡単な教程, 1963)
![]() と置くと,
と置くと,
![]() . 即ち
. 即ち
![]() . ところが, 加比の理より
. ところが, 加比の理より
![]() . 従って
. 従って![]()
1 が並んだ整数 (例えば 111111) をレピュニット数というのだそうである。 (Repunit = repeated units らしい。 こことかここを参照のこと)
平面上の全ての凸図形は内部の一点から出るk本の半直線によって外周と面積とを同時に k 分割することが出来る。 [Discrete and Computational Geometry, Lecture Note in Computer Science, No. 1763, Springer]
n 個の実数 a1, a2, … , an がある。これらの
n 次の基本対称式を bn としよう。このとき
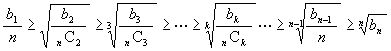
が成立する。
その証明は,
先ず相加平均と相乗平均の関係を用いて最後の不等式, 即ち
![]() を出し,
を出し,
![]() と置くときの, f', f", …
について論じることによって得られる。 [藤原松三郎:
代数学, 第 8 章演習問題 5]
と置くときの, f', f", …
について論じることによって得られる。 [藤原松三郎:
代数学, 第 8 章演習問題 5]
p を正の整数とするとき
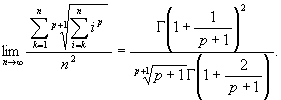
[仁平政一, 数学セミナー (8), 2001]
証明)
函数y = xpで積分と区分求積とを比較すると
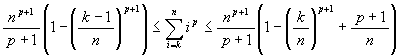
を得る。これを用いて挟み撃ちすると 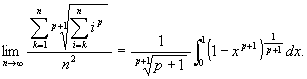
だが, これから u = xp+1 と置いて beta 函数の公式を用いると上記の式を得る。
(証明を見ると分かるように実は p は正の実数でありさえすればよい)
特に p=1 とすると ![]() , 又
p が正の整数であるならば
, 又
p が正の整数であるならば 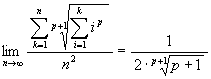 であり,
特に p = 1 である時
であり,
特に p = 1 である時 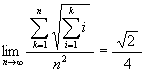 である。
である。
Fibonacci とは "Bonacci 家の子" という意味である。
所謂 Fibonacci 数列の一般項を an と書くことにすれば m|n ⇔ am|an が成り立つ。 (和田秀男 「数の世界」, 岩波書店)
Rayleigh の定理 (「音響論」 から)
A={[nα]: n∈N}, B={[nβ]: n∈N} に関し A∩B =
Æ, A∪B = N となるための必要且つ十分な条件は
α > 1 なる無理数で 1/α + 1/β = 1
となることである。
証明は共立全書のヴィノグラードフ著 「整数論入門」
を見よ。
五次方程式が代数的に説けないことの最初の手がかりを得たのはルフィニであり, 1799 -- 1813 に発表した幾つかの長大な論文により S5 の研究からそれに気付いた。
Homology 論を生んだのは Cauchy の積分定理で, H. Poincaré Analysisi situs (1895) による。
![]()
![]()
和 Σk=1nkm = fm(n) とすると, 方程式
fm(n) = 0 の解は, n = -1/2 に関して対称である。 実はfm(-1-x)
= fm(x) である。
![]() と F(x, t) + F(-1-x) = -1
なることの証明をすればよい。
と F(x, t) + F(-1-x) = -1
なることの証明をすればよい。
尚, fm(n) に関しては, m > 1 では, m が偶数のとき n(n+1)(n + 1/2)
で割り切れ, m が奇数の時は n2(n + 1)2
で割り切れることが知られている。
野海正俊
母函数と出会う
論集 現代の母函数
Digital 信号処理の世界では sinc t = (sin t)/t という函数が活躍する。
記号 ≡ と ∽ は Leibniz によるそうである。
Kepler 予想 「等しい大きさの球を充填していくとき, 面心立方格子より高密度の配置は存在しない」(1611) の証明は Thomas C. Hales によってなされている (1998, http://www.math.lsa.umich.edu/~hales/)。
物理の問題で n 体問題というのがあるが, それについて幾つかの発展があり Barcelona の C. Simo の site に見ることが出来る。