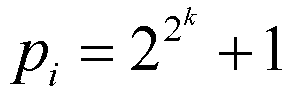 ,
,Mayu told me (on 21:03:28 Monday, 1st January 2001 on my BBS) a story in the TV drama Yamato-Nadeshiko, which is how to draw a regular heptadecagon when a wedding cake equally divided into 68 parts.
Since we see that 68 = (2 square) times 17, it is needed that 360 degree must be divided equally into 17 parts. But I think it is witless in the wedding reception. Do almost Japanese think mathematicians are so witless?
First we clarify what is the construction problem in mathematics:
The construction (drawing) in mathematics is the drawing that you can use only a ruler (without scale) and a compass. You should finish drawing finite times after using the given segment of line to the following four operations:
If you allow other operations, you can draw any figures: e.g. you can trisect a given angle with a trisect ruler, draw an ellipse with an ellipse-ruler, a parabola with a parabola-ruler.
Owing to G.Mohr and L. Mascheroni, you can draw a figure only with a compass if you can draw a compass and a ruler (of course you cannot draw an actual line); and owing to J.-V. Poncelet and Steiner, you can draw only with a ruler if a circle and its center is given and if you can draw a compass and a ruler (of course you cannot draw an actual circle).
You may have a question why some figures can be drawn and some cannot with a compass and a ruler?
You use a complex plane (or Gauss plane), without loss of generalities, the given segment can be the interval [0, 1] on the real axe (the x-axe of the xy-plane). They are the same that you draw figures with the methods above and that taking points using Pythagorean theorem. Hence the length of the constructible segments are the rational numbers and iterating square root and their additions, subtractions and multiplications. The same applies to the coordinates of the points on the plane, which can be seen as the complex numbers (with the correspondence (x, y) with x + iy, where i is the imaginary unit). So you cannot draw using the (imaginary) number out of the finite extension of the quadratic extension (in algebraic word)
Since in Euclid era, a number means a segment which can be drawn, the classification of the numbers is very complicated in Euclid's Elements. Such complications are prevent the reader.
What regular polygon can be drawn?
As we mention above, the construction problem is the completely same as the extension theory of the rational number field in the complex plane. The possibility of drawing a regular polygon is decided to investigate the extension degree of Q(zeta) where zeta = cos(2pi/n) + i sin(2pi/n). Owing C. F. Gauss it is known that you can draw a regular n-gon if and only if the n is decomposed to prime factors as n = 2mp1p2p3…pr where every distinct pi is odd and
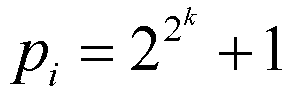 ,
,
which are called Fermat primes. Fermat primes are known only k = 0, 1, 2, 3, 4 that is p = 3, 5, 17, 257, 65537.
Japanese mathematician TERASAKA, Hidetaka. says in his book Hi-Euclid Kikagaku no Sekai (the World of the Non-Euclidian Geometry), Kodansha:
So we can construct a regular heptadecagon. How about a regular 257-gon?
--- Since the number 257 is also a prime, you can construct it, of course. But since Euclid era, the constructible regular n-gon, where n is odd, are only 3, 5, 15. Therefore it is a sensation that a regular heptadecagon is constructible. The number 257 is too big to be surprised. 17 is a handy size.
translated by myself
You know the construction of regular triangle. If you don't know the construction of regular pentagon, see this page (Japanese).
The approximately construction of the regular n-gon is also well known. (Japanese)
Let's take up the main topic.
Mentioning above, Carl Friedrich Gauss (30 April 1777 -- 23 February 1855) found that the regular Fermat prime polygons are constructible in the morning of the 30th March, 1796. He was only 19 years old. He found such a fact suddenly when he woke up. This discovery let him decide to be a mathematician.
It is enough to show that cos(2pi/17) can express to use only square roots and rational numbers (without cube roots or 5th roots of rational numbers). (Although I tried to solve the equation of degree 17, x17 - 1 = 0, the solution is too complicated to show here.)
Let phi (φ) be 2pi/17, and let the four numbers be
a = cos phi + cos 4phi,
b = cos 2phi + cos 8phi,
c = cos 3phi + cos 5phi,
d = cos 6phi + cos 7phi.
You may wonder these replacements are strange. As the number a, the angles are phi and its four times; as b, the anbles are 2phi and its four times. As c, the four times of 3phi must be 12phi, but since the cosine function has the property that cos n(phi) = cos(17 - n)phi, cos 12phi = cos(17 - 12)phi = cos 5phi. Also as d, since four times of 6phi = 24phi = (17 + 7)phi, and 17phi = 2pi is the period of the cosine function.
And let:
e = a + b,
f = c + d,
then since cos n(phi) = cos(17 - n)phi,
e + f = cos phi + cos 2phi + cos 3phi + cos 4phi + cos 5phi + cos 6phi + cos
7phi +cos 8phi
= (2cos phi + 2cos 2phi + 2cos 3phi + 2cos 4phi + 2cos 5phi + 2cos 6phi + 2cos
7phi + cos 8phi)/2
= ((cos phi + cos 16phi) + (cos 2phi + cos 15phi) + (cos 3phi + cos 14phi) + (cos
4phi + cos 13phi) + (cos 5phi + cos 12phi) + (cos 6phi + cos 11phi) + (cos 7phi
+ cos 10phi) + (cos 8phi + cos 9phi))/2
= (cos phi + cos 2phi + cos 3phi + cos 4phi + cos 5phi + cos 6phi + cos 7phi +
cos 8phi + cos 9phi + cos 10phi + cos 11phi + cos 12phi + cos 13phi + cos 14phi
+ cos 15phi + cos 16phi)/2.
We introduce the formula
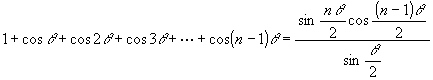 ,
,
which is equivalent to the formula
![]()
to get the both sides multiplied by sin (theta/2). The proof of this formula is:
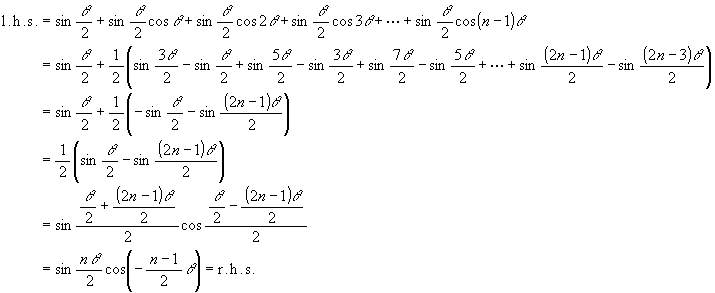
(we use the "products to sums" formula to get 2nd line, and the "sum to product" formula to get 5th line.)
By this formula, we get
e + f = (cos phi + cos 2phi + cos 3phi + cos 4phi + cos 5phi + cos 6phi + cos 7phi + cos 8phi + cos 9phi + cos 10phi + cos 11phi + cos 12phi + cos 13phi + cos 14phi + cos
15phi + cos 16phi)/2
= (1 + cos phi + cos 2phi + cos 3phi + cos 4phi + cos 5phi + cos 6phi + cos 7phi + cos
8phi + cos 9phi + cos 10phi + cos 11phi + cos 12phi + cos 13phi + cos 14phi + cos 15phi
+ cos 16phi)/2 - 1/2
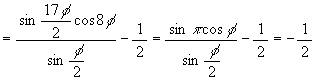
(we use the fact 17phi is 2pi at the last line), that is
e + f = -1/2 …… (1).
By the "product to sum" formula
2cos alpha cos beta = cos(alpha + beta) + cos (alpha - beta),
and cos n(phi) = cos(17 - n)phi, we get
2ab = e + f = -1/2,
2ac = 2a + b + d,
2ad = b + c + 2d,
2bc = a + 2c + d,
2bd = a + 2b + c,
2cd = e + f = -1/2
(its proof).
Therefore
2ef = 2(a + b)(c + d)
= 2ac + 2ad + 2bc + 2bd = (2a + b + d) + (b + c + 2d) + (a + 2c + d) + (a + 2b +
c)
= 4a + 4b + 4c + 4d = 4(a + b + c + d) = 4(e + f) = 4 · (-1/2)
= -2
that is
ef = -1 …… (2).
By the equations (1) and (2), the numbers e and f are the solution of the quadratic equation of x
![]()
that is 2x2 + x - 2 = 0. And we get
![]() .
.
Since the numbers a and b satisfy the equations a + b = e, ab = (e + f)/2 = -1/4, they are the solutions of the quadratic equation of x
![]() .
.
We get
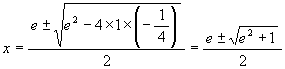 .
We already got the value of e, so we get
.
We already got the value of e, so we get
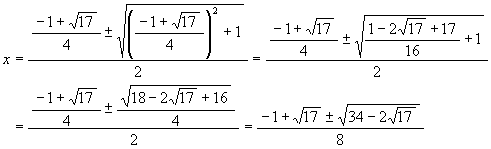
We must decide the double sign (±) above. Since the cosine function is
strictly monotonous decreasing on the interval [0, pi],
a - b = (cos phi + cos 4phi) - (cos 2phi + cos 8phi)
= (cos phi - cos 2phi) + (cos 4phi
- cos 8phi) > 0.
Therefore the solution of + sign is the number a, and the other is the number b.
Similarly, since the numbers c and d satisfy the equations c + d = f, cd = -1/4,
we get
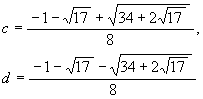 .
.
Finally we calculate cos phi and cos 4phi. Since cos phi + cos 4phi = a and since
by the "product to sum" formula
![]() ,
,
these are the solutions of the quadratic equation of x
![]() .
.
Since clearly cos phi > cos 4phi, we get
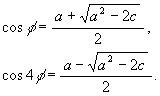
Since 2cos phi cos 4phi = c and the "power reduction" formula 2cos2theta
= 1+ cos 2theta, we get
2a2 = 2(cos phi + cos 4phi)2
= 2(cos2 phi + cos2 4phi + 2cos phi cos 4phi)
= 2cos2 phi + 2cos2 4phi +4cos phi cos 4phi
= 1 + cos 2phi + 1 + cos 8phi + 2c
= 2 + cos 2 phi + cos 8phi + 2c
= 2 + b + 2c.
Finally we get
This shows that cos phi can express only by rational numbers and square roots. Therefore cos phi is constructible hence a regular heptadecagon is.
About the actual construction of a regular heptadecagon, The letter to Gauss at 22nd March 1802 written by Pfaff shows "Prof. so-and-so who is the representative of the pure geometrical method in Germany" got the method. The documented first constructor is the captain of the canon soldier, von Huguenin.
The construction of a regular heptadecagon (Japanese).
The solution of the equation of degree 257 x257 = 1 can be found Richelot, De resolutione algebraica aequationis X257 = 1, Crelle's Journal 9.
By Literka (Mr. Boguslaw Tomaszewski), Chris Becker shows sin(pi/257). Literka has pages of calculation of the value of trigonometric functions of angle pi/257. I had communications with him in 4th -- 14th April, 2004 and give a few suggestions.
[Proof]
Proof of
2ab = e + f = -1/2,
2ac = 2a + b + d,
2ad = b + c + 2d,
2bc = a + 2c + d,
2bd = a + 2b + c,
2cd = e + f = -1/2.
Since phi = 2pi/17; and since
a = cos phi + cos 4phi,
b = cos 2phi + cos 8phi,
c = cos 3phi + cos 5phi,
d = cos 6phi + cos 7phi;
using cos n(phi) = cos (17 - n)phi;
2ab = 2(cos phi + cos 4phi)(cos 2phi + cos 8phi)
= 2cos phi cos 2phi + 2cos phi cos 8phi + 2cos 4phi cos 2phi + 2cos 4phi cos
8phi
= cos 3phi + cos phi + cos 9phi + cos 7phi + cos 6phi + cos 2phi + cos 12phi + cos
4phi
= cos 3phi + cos phi + cos 8phi + cos 7phi + cos 6phi + cos 2phi + cos 5phi + cos
4phi
= e + f.
2ac = 2(cos phi + cos 4phi)(cos 3phi + cos 5phi)
= 2cos phi cos 3phi + 2cos phi cos 5phi + 2cos 4phi cos 3phi + 2cos 4phi cos
5phi
= cos 4phi + cos 2phi + cos 6phi + cos 4phi + cos 7phi + cos phi + cos 9phi + cos
phi
= cos 4phi + cos 2phi + cos 6phi + cos 4phi + cos 7phi + cos phi + cos 8phi + cos
phi
= 2(cos phi+ cos 4phi) + cos 2phi + cos 8phi + cos 6phi + cos 7phi
= 2a + b + d.
2ad = 2(cos phi + cos 4phi)(cos 6phi + cos 7phi)
= 2cos phi cos 6phi + 2cos phi cos 7phi + 2cos 4phi cos 6phi + 2cos 4phi cos
7phi
= cos 7phi + cos 5phi + cos 8phi + cos 6phi + cos 10phi + cos 2phi + cos 11phi + cos
3phi
= cos 7phi + cos 5phi + cos 8 phi + cos 6phi + cos 7phi + cos 2phi + cos 6phi + cos
3phi
= cos 2phi + cos 8phi + cos 3phi + cos 5phi + 2(cos 6phi + cos 7 phi)
= b + c + 2d.
2bc = 2(cos 2phi + cos 8phi)(cos 3phi + cos 5phi)
= 2cos 2phi cos 3phi + 2cos 2phi cos 5phi + 2cos 8phi cos 3phi + 2cos 8phi cos
5phi
= cos 5phi + cos phi + cos 7 phi + cos 3phi + cos 11 phi + cos 5phi + cos 13phi + cos
3phi
= cos 5phi + cos phi + cos 7 phi + cos 3phi + cos 6phi + cos 5phi + cos 4phi + cos
3phi
= cos phi + cos 4 phi + 2(cos 3phi + cos 5phi) + cos 6 phi + cos 7phi
= a + 2c + d.
2bd = 2(cos 2phi + cos 8phi)(cos 6phi + cos 7phi)
= 2cos 2phi cos 6phi + 2cos 2phi cos 7phi + 2cos 8phi cos 6phi + 2cos 8phi cos
7phi
= cos 8phi + cos 4 phi + cos 9phi + cos 5phi + cos 14phi + cos 2phi + cos 15phi + cos
phi
= cos 8phi + cos 4 phi + cos 8phi + cos 5phi + cos 3phi + cos 2phi + cos 2phi + cos
phi
= cos phi + cos 4 phi + 2(cos 2phi + cos 8phi) + cos 3 phi + cos 5phi
= a + 2b + c.
2cd = 2(cos 3phi + cos 5phi)(cos 6phi + cos 7phi)
= 2cos 3phi cos 6phi + 2cos 3phi cos 7phi + 2cos 5phi cos 6phi + 2cos 5phi cos
7phi
= cos 9phi + cos 3phi + cos 10 phi + cos 4 phi + cos 11 phi + cos phi + cos 12phi + cos
2phi
= cos 8phi + cos 3phi + cos 7phi + cos 4 phi + cos 6 phi + cos phi + cos 5phi + cos
2phi
= e + f.
Back to Japanese page.
Top page of this site (Japanese).