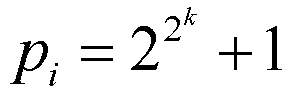
麻由さんに web 上で聞いた話 --- BBS で 21:03:28 Monday, 1st January 2001 --- によると, TV ドラマ 「やまとなでしこ」 でウエディングケーキを 68 人で分けるときに, 正十七角形の作図に関して言及されたのだそうである。
68 = 22×17 であるから, 確かに等分しようと思えば, どうしたって 360 度を 17 等分する必要にせまられるわけであろうが, しかし結婚披露宴の話題としては随分無粋な話題である。 数学者という奴は無粋な奴と相場が決まっているのであろうか (笑)。
先ず数学に於ける 「作図問題 construction problem」 というものを明確にしておこう。
作図とは, 簡単に言うと 「(目盛りのついてない) 定規とコンパスのみによって作図する」 ということである。 もう少しちゃんというと, 与えられた線分の描いてある一つの定められた紙 (平面) の上で, 最初に与えられた線分から次の四つの操作を有限回繰り返して描き終われることをいう。
これ以外の操作をいろいろ加えると, 何だって描けてしまう。 例えば角の三等分だって三等分定規ってのを使うと出来る。 楕円や放物線だって, それぞれを描く為の専門の道具があるのでそれを使うと描ける。
因みに, G. Mohr と L. Mascheroni に拠れば, 定規とコンパスで作図できる図形はすべてコンパスだけで作図できる (但し実際に直線を引くことは断念する)。 又 J.-V. Poncelet と Steiner に拠れば, 定規とコンパスで作図できる図形は, 最初に一つの円とその中心とが与えられてあれば定規だけで作図できる (但し実際に円を描くことは断念する)。
しかし, そもそもどうして定規とコンパスだけで描こうとすると, ある図形が描けたり描けなかったりするのか ?
複素平面というものを考えて, 最初に与えられた線分は, 実軸 (分からなければ xy 平面の x 軸と思って良い) の原点と 1 とを結んだものと考えて良い。 これからコンパスと定規を使って平面上に図形を描いて行くのは, 三平方の定理を使って, この平面上に点を採って行くのと同じことである。 従って, 作れる線分の長さは有理数とそれに √ をつけたりしていく数 (とそれらの積と和, 差) に限られる。平面上の座標も同様である。 これ (= 座標) を複素数だと思うことが出来て, 代数学の体の理論の言葉を使うと, 有理数体 Q の二次拡大の有限回の繰り返しで到達できる体の中にない数を使っているような作図は出来ないということになる。
ユークリッドの時代には, 数とは即ち作図可能な線分のことだったから, この辺の分類は非常にうるさくて, 所謂原論の第十巻には, これこれの線分は作図可能ということが延々と書き連ねてあって読むのが嫌になる (笑)。
正 n 角形のうちどういうのが実際に作図可能なのだろうか ?
先程書いたように, 作図の問題は複素平面上の体の拡大の理論と同じである。 正 n 角形を作図するということの可能性は, 有理数体 Q を基礎体として, ζ = cos(2π/n) + i sin(2π/n) を添加した体 Q(ζ) の拡大次数というものを調べるのと等しいことだということが分かっている。 Galois (ガロア) 理論の細かい所は除くと, n = 2νp1p2p3…pr という素因数分解を持ち, 各々異なる各奇素数 pi について
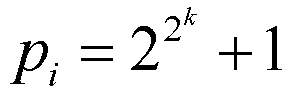
という形をしたものに限って作図可能ということが分かっている。 この形の素数を Fermat number (フェルマ数) という。 今の所 k = 0, 1, 2, 3, 4 のところしか素数になることが分かっていない。 それらは p = 3, 5, 17, 257, 65537 である。
数学者寺坂英孝は 「非ユークリッド幾何学の世界」, 講談社ブルーバックス B312 でこんな事を言っている。
だから正 17 角形が作図できるのですね。 正 257 角形はどうなんですか。
--- 257 も素数だから, 勿論作図できる。 しかしユークリッドの昔から正 n 角形で作図できるのは, n が奇数のときは 3, 5, 15 だけ位だったから, 素数の正 17 角形が定規とコンパスで作図できるというのはセンセーションだったのだ。 257 角形じゃ数が大き過ぎて, 驚き様がないやね。 上手い所に運良く 17 という数があったものだ。
正三角形の作図は誰でも知っているだろうが正五角形の作図はあまり知っている人がいないだろう。 それは別項に書くことにする。
尚, 近似的な正 n 角形の作図は良く知られている。 それも別項に書く。
いよいよ本題。
Fermat 数の正多角形ならば作図可能であることに気付いたのはかの Carl Friedlich Gauß (カール・フリードリヒ・ガウス, 30 April 1777 -- 23 February 1855) 大先生である。 発見したのは 1796 年 3 月 30 日の朝。 19 歳のとき, 目覚めて起きようとした時に忽然と思いついたのであるという。 この発見がガウスをして数学者を志させたということだ。
さて, 正 17 角形が作図可能であることをいうには, cos(2π/17) が三乗根とか, 五乗根とかを用いずに高々 √ だけを用いて書ける無理数だということを実際に書いて見せればいい。 --- 因みに 17 次方程式 x17 - 1 = 0 を実際に解いてみようと思ったらものすごく大変な式になったので紹介するのもやめておく。
φ = 2π/17 として以下のように置こう。
a = cos φ + cos 4φ,
b = cos 2φ + cos 8φ,
c = cos 3φ + cos 5φ,
d = cos 6φ + cos 7φ.
慣れない人は一寸変な置き方だと思うかもしれないが, a については φ とその 4 倍, b についても 2φ とその 4 倍である。 3φ の 4 倍は 12φ であるが, 余弦函数の性質により cos nφ = cos (17 - n)φ という性質が成り立つので, c についても同様に 4 倍の関係が成り立っているのである。 又, 4×6φ = 24φ = (17 + 7)φ であり, 17φ = 2π は余弦函数の周期だから, d についても 4 倍の関係が成り立っている。
更に
e = a + b,
f = c + d
と置くと, cos nφ = cos (17 - n)φ に注意して
e + f = cos φ + cos 2φ + cos 3φ + cos 4φ + cos 5φ + cos 6φ + cos 7φ +cos
8φ
= (2cos φ + 2cos 2φ + 2cos 3φ + 2cos 4φ + 2cos 5φ + 2cos 6φ + 2cos 7φ +
cos 8φ)/2
= ((cos φ + cos 16φ) + (cos 2φ + cos 15φ) + (cos 3φ + cos 14φ) + (cos 4φ
+ cos 13φ) + (cos 5φ + cos 12φ) + (cos 6φ + cos 11φ) + (cos 7φ + cos 10φ)
+ (cos 8φ + cos 9φ))/2
= (cos φ + cos 2φ + cos 3φ + cos 4φ + cos 5φ + cos 6φ + cos 7φ + cos 8φ
+ cos 9φ + cos 10φ + cos 11φ + cos 12φ + cos 13φ + cos 14φ + cos 15φ +
cos 16φ)/2
ここで一般的な公式
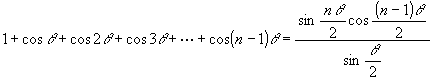
を紹介しておく。証明は両辺を sin (θ/2) 倍して
![]()
の形で証明すれば良い。 (下記で l.h.s. = left hand side = 左辺,
r.h.s. = right hand side = 右辺)
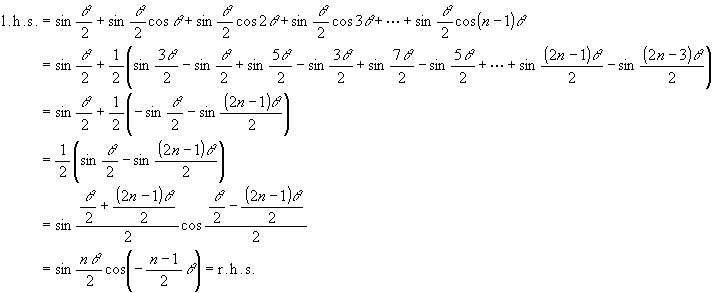
一行目から二行目で, 積を和に変える公式を用いている。又四行目から五行目では逆に和を積に変える公式を用いている。
さて, この公式を用いてやると
e + f = (cos φ + cos 2φ + cos 3φ + cos 4φ + cos 5φ + cos 6φ + cos 7φ +
cos 8φ + cos 9φ + cos 10φ + cos 11φ + cos 12φ + cos 13φ + cos 14φ + cos
15φ + cos 16φ)/2
= (1 + cos φ + cos 2φ + cos 3φ + cos 4φ + cos 5φ + cos 6φ + cos 7φ + cos
8φ + cos 9φ + cos 10φ + cos 11φ + cos 12φ + cos 13φ + cos 14φ + cos 15φ
+ cos 16φ)/2 - 1/2
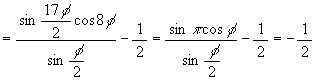
最後のところで 17φ = 2πを用いている。
重要なのでもう一度書くと
e + f = -1/2 …… (1).
若干計算を省略するが, 積を和に変える公式
2cos αcos β = cos(α + β) + cos (α - β)
と先程の cos nφ = cos (17 - n)φ を用いると次の 6
つの式が得られる (証明)
2ab = e + f = -1/2,
2ac = 2a + b + d,
2ad = b + c + 2d,
2bc = a + 2c + d,
2bd = a + 2b + c,
2cd = e + f = -1/2.
よって,
2ef = 2(a + b)(c + d)
= 2ac + 2ad + 2bc + 2bd = (2a + b + d) + (b + c + 2d) + (a + 2c + d) + (a + 2b +
c)
= 4a + 4b + 4c + 4d = 4(a + b + c + d) = 4(e + f) = 4 × (-1/2)
= -2
即ち
ef = -1 …… (2).
従って (1), (2) から二次方程式の解と係数の関係を用いて e, f は二次方程式
![]()
言い換えれば 2x2 + x - 2 = 0 の解。 解の公式を用いてこれを解けば
![]()
ここで一寸だけ話がいいかげんになるが,
e = a + b = cos φ + cos 4φ + cos 2φ + cos 8φ,
f = c + d = cos 3φ + cos 5φ + cos 6φ + cos 7φ,
であったが, φ = 2π/17 であったことを思い出せば, φ, 2φ, 3φ, 4φ
は第一象限の角, 5φ, 6φ, 7φ, 8φ は第二象限の角である。
第一象限の角の余弦は +, 第二象限の角の余弦は -
であったことを思い出せば, 大体 e > 0, f < 0
であることが分かる。 つまり先程の解で, 複号 ± は e が +,
f が - である。 改めて書けば
![]()
である。
さて, a と b は a + b = e, ab = (e + f)/2 = -1/4 を満たしているから再び二次方程式の解と係数の関係から方程式
![]()
の解である。 解の公式に入れて
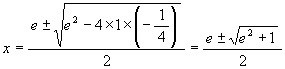
であるが, これに先程の結果を入れると,
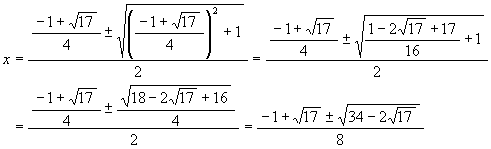
となる。 複号の問題であるが, 余弦函数が 0 から π 迄
(狭義) 単調減少であることを用いると,
a - b = (cos φ + cos 4φ) - (cos 2φ + cos 8φ) = (cos φ - cos 2φ) + (cos 4φ
- cos 8φ) > 0
だから, + の方がa で, - の方が b である。
同様に c, d は c + d = f, cd = -1/4 だから,
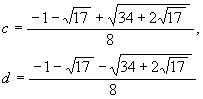
を得る。
さて最後に (そして求めたかった) cos φ と付随して cos 4φ
の値であるが, cos φ + cos 4φ = a で, 積を和に変える公式より
![]()
であるので, これらは
![]()
の解。 解の公式を用いて (又明らかに cos φ > cos 4φ であるから)
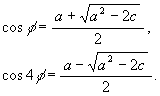
ところで先程の 2cos φcos 4φ = c と, 半角の公式 2cos2θ
= 1+ cos 2θ によって
2a2 = 2(cos φ + cos 4φ)2
= 2(cos2 φ + cos2 4φ + 2cos φcos 4φ)
= 2cos2 φ + 2cos2 4φ +4cos φcos 4φ
= 1 + cos 2φ + 1 + cos 8φ + 2c
= 2 + cos 2 φ + cos 8φ + 2c
= 2 + b + 2c.
よって
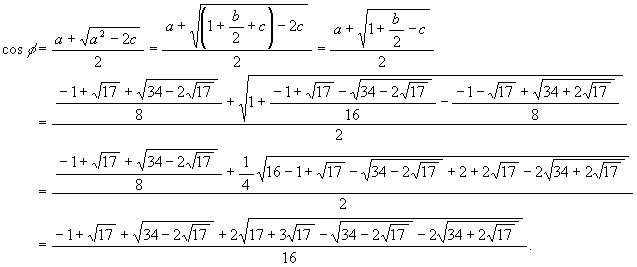
となってめでたく, cos φ が √
だけで書けることが分かった。 よって cos φ は作図可能。
従って正 17 角形も作図可能である。
さて, 実際の作図法であるが, 実際にその方法を示したのは Pfaff という人が 1802 年 3 月 22 日付で Gauß 宛てに書いた書簡で, 「ドイツに於ける純幾何学的方法の代表者というべき」 教授何某が考えたのが最初らしい。 文献に残っているのは 1803 年砲兵大尉 von Huguenin なる人物らしい。
正 17 角形の作図は大変なので別項を改めて書く。 (しかしスキャナがないので等分の間 pending)
因みに x257 = 1 の解については Richelot, De resolutione algebraica aequationis X257 = 1, Crelle's Journal 9 に出ているとのことである。
Literka (Boguslaw Tomaszewski 氏) に拠ると Chris Becker 氏が sin(π/257) の値を upload しているそうである。 Literka と 4th -- 14th April, 2004 頃 communicate を取って若干の suggestions をしたところ, この計算方法についての page を書き始めたようである。 今後の解析が待たれる。
Saturday, 12th June, 2004.
参考文献:
高木貞治, 近世数学史談, 第三版, 共立出版, 1970, 復刻版 1996.
高木貞治, 代数学講義, 共立出版。
Emil Artin (アルティン), ガロア理論入門, 寺田文行訳,
東京図書, 1974.
龍山一郎, 三次方程式と三角関数は親戚 ?
The Thirteen Books of Eucilid's Elements by Sir Thomas L. Heath, &al, 2nd
ed. vol. III, Dover.
園正造, 方程式論, 至文堂, 1929.
作図問題に関しては
(入手可能かどうかはなはだ疑問だが):
スモゴルジェフスキー, コストフスキー,
定木による作図・コンパスによる作図, 数学新書,
東京図書。
窪田忠彦, 初等幾何学作図題, 東京内田老鶴圃。
佐々木重夫, 幾何入門, 岩波全書。
窪田忠彦, 近世幾何学, 岩波書店。